7.2 Dvojné a dvojnásobné integrály na obecnějších množinách

Definice

Nechť  M  je podmnožina nějakého dvojrozměrného intervalu  .  Na tomto intervalu definujme funkci

      pro ,

     pro .

Pokud existuje  ,  nazveme množinu  M  (Riemannovsky) měřitelnou a odpovídající dvojný integrál mírou (plošným obsahem) této množiny.

Poznámka

Všimněte si, že míra intervalu    je  podle očekávání  .

Věta

Množiny

,

,

kde  , ,  a   jsou spojité funkce na intervalech   a ,  jsou měřitelné.

Definice [1]

Nechť    (I je uzavřený interval z  je měřitelná množina a funkce    je na ní definována. Na intervalu  I  definujme novou funkci

        pro ,

                pro .

Pokud existuje  ,  řekneme, že funkce  f  je na množině  M  Riemannovsky integrovatelná, a odpovídající integrál nazveme dvojným Riemannovým integrálem funkce  f  na množině  M.

Pro dvojné integrály na obecných měřitelných množinách budeme ve shodě s výše uvedeným značením používat symbol .

Věta (Fubiniova) [2]

Nechť  N1 a  N2  jsou výše zavedené měřitelné množiny a    nechť je integrovatelná funkce na těchto množinách. Pak platí

 ,

.

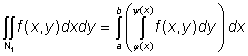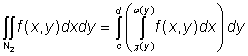Poznámka

I v případě obecnějších množin  N1a N2  je tedy možno dvojné integrály počítat pomocí integrálů jednoduchých, pokud ovšem víme, že příslušný dvojný integrál existuje. To je opět zaručeno například pro spojité funkce.

[1] I tato definice je v zájmu zachování jednoduchosti výkladu velmi zjednodušená. Podrobnější informaci může zájemce opět najít ve specializované literatuře.

[2] Všechny věty, které nesou v této i další kapitole označení Fubiniova jsou speciálními variantami jediné obecné věty o rozkladu vícerozměrných integrálů na integrály násobné. V matematické literatuře je tato věta obvykle nazývána větou Fubiniovou, a proto jsme takové označení zachovali bez jakéhokoliv dalšího rozlišení i pro speciální formulace, jak je uvádíme v tomto skriptu.