7.1 Dvojné a dvojnásobné integrály na dvojrozměrných intervalech

Definice

Pod uzavřeným intervalem z  rozumíme kartézský součin  .

Definice

Nechť    je uzavřený interval z    a  ,  resp.    jsou dělení intervalů  ,  resp.  . Pak množinu

nazveme dělením intervalu  I  a číslo

normou dělení  D.

Definice

Nechť    je dělení uzavřeného intervalu  I  z   a    množina uspořádaných dvojic reálných čísel takových, že    a  . Dále nechť je  f  omezená funkce na intervalu  I [1]. Pak součet

nazveme Riemannovou integrální sumou funkce  f  pro dělení  D  a  množinu čísel  z.

Definice

Nechť    je posloupnost dělení intervalu  I,  jejichž norma konverguje k nule, , a zN posloupnost množin dvojic čísel   z předcházející definice přiřazených dělením  . Funkce    nechť je definována a omezená na intervalu  I.  Existuje-li pro všechny takové posloupnosti jejich společná limita [2]

,

nazveme tuto limitu dvojným Riemannovým integrálem funkce    na intervalu  I.   Samotnou funkci pak nazveme integrovatelnou na intervalu  I.

Pro dvojné integrály na intervalu    používáme obvykle označení  [3]  nebo  .

Věta (Fubiniova)

Nechť je funkce    integrovatelná na intervalu  .  Pak platí

.

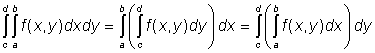Poznámka

Podle Fubiniovy věty můžeme tedy dvojný integrál na dvojrozměrném intervalu počítat jako dvojici integrálů jednoduchých, přičemž na pořadí integrace nezáleží. Musíme ovšem zaručit, že hledaný dvojný integrál existuje, což je možné například pro spojité integrandy.

Integrály na pravé straně rovnosti nazýváme zpravidla dvojnásobnými.

[1] Tj. existuje takové nezáporné číslo  K,  že pro každou dvojici [x,y] z intervalu  I  platí  .

[2] Viz Apendix A3.

[3] V námi používané konvenci odpovídá vnitřní integrál vnitřnímu diferenciálu a vnější integrál diferenciálu vnějšímu.