11.3 Křivkový integrál druhého druhu

Křivkové integrály prvního a druhého druhu jsou si velmi blízké. Níže si zejména všimněte, jak mnohé věty formulované pro integrály druhého druhu odpovídají větám předcházející kapitoly.

Definice

Nechť    je křivka třídy C₁ a    vektorové pole spojité na nějakém okolí každého bodu geometrického obrazu  .  Pak předpisem

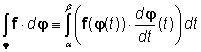
definujeme křivkový integrál druhého druhu pole  f  po křivce  j.

Je-li křivka  j uzavřená, používáme pro obvykle odpovídající křivkový integrál symbol

.

Poznámka

V definičním vztahu stojí v závorce integrandu na pravé straně skalární součin dvou vektorů z , tedy

.

Formálním porovnáním pravé a levé strany definičního vztahu pro křivkový integrál druhého druhu získáme symbolickou rovnost  .  Infinitezimální vektor  dj  je tedy v každém bodě tečný ke křivce  j  a míří do směru, v němž hodnota parametru  t  roste. Jeho velikost odpovídá navíc s přesností do prvního řádu délce oblouku této křivky na intervalu  . Vektor  dj můžeme proto s přesností do prvního řádu interpretovat jako infinitezimální orientovaný oblouk křivky  j  na intervalu  .

Poznámka

Velmi názorná je fyzikální interpretace křivkového integrálu druhého druhu. Chápeme-li totiž křivku  j jako trajektorii opisovanou hmotným bodem v prostoru (pak ovšem ) a vektorové pole  f  jako pole vnějších sil na tento bod působících, pak odpovídající křivkový integrál není nic jiného než práce vykonaná těmito silami.

Definice

Nechť    je vektorové pole spojité na nějakém okolí každého bodu geometrického obrazu křivky  , která je na tomto intervalu po částech třídy C₁. Existuje tedy takové dělení   intervalu  , že    má na každém dělicím intervalu ,  ,  nenulovou spojitou první derivaci. Pak pod křivkovým integrálem druhého druhu pole  f  po křivce  j  rozumíme

.
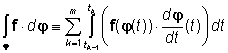