11.2 Křivkový integrál prvního druhu

Definice (křivkový integrál prvního druhu pro křivky C₁)

Nechť    je křivka třídy C₁ a    reálná funkce n reálných proměnných, jež je spojitá na nějakém okolí každého bodu geometrického obrazu  .  Pak předpisem

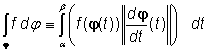
definujeme křivkový integrál prvního druhu funkce  f  po křivce  j. [1]

Je-li křivka  j  uzavřená, používáme zpravidla pro odpovídající křivkový integrál symbol .

Poznámka

Formálním porovnáním pravé a levé strany definičního vztahu pro křivkový integrál prvního druhu získáme symbolickou rovnost  nebo též  .  Diferenciál  dj  na levé straně odpovídá tedy délce infinitezimálního oblouku křivky  j  na intervalu   a integrál

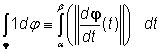
délce křivky  .

Věta (aditivita křivkového integrálu prvního druhu vůči skládání křivek)

Nechť křivky j a y jsou na intervalech  a  třídy C1 a splňují .  Pak platí

.

Definice (křivkový integrál prvního druhu pro křivky po částech C₁)

Nechť    je reálná funkce spojitá na nějakém okolí každého bodu geometrického obrazu křivky  ,  která je na tomto intervalu po částech třídy C₁. Existuje tedy takové dělení   intervalu  , že    má na každém dělicím intervalu ,  ,  nenulovou spojitou první derivaci. Pak pod křivkovým integrálem prvního druhu funkce  f  po křivce    rozumíme

.

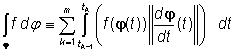Poznámka

Aditivita integrálu 1. druhu pro křivky třídy C₁ zaručuje, že výše uvedená definice je korektní. Jako dělicí body  t_k  musíme vždy vybrat především ty, v nichž křivka  j  nemá spojitou první derivaci. Přidáme-li k nim i takové, v nichž tato křivka spojitou první derivaci má, pravá strana výše uvedené rovnosti se díky zmíněné aditivitě nezmění.