![]() Hmotnost nekonečně tenkého vlákna
Hmotnost nekonečně tenkého vlákna
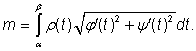 |
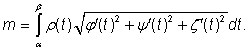 |
![]() Definice
Definice
Nekonečně tenké vlákno reprezentujeme v rovině parametricky
zadanou křivkou ![]() a
a
![]() ,
kde parametr
,
kde parametr ![]() a
vektorová funkce
a
vektorová funkce ![]() je
prostá na
je
prostá na ![]() [1].
Označme
[1].
Označme ![]() hmotnost
malé části vlákna, pro kterou parametr nabývá hodnot z intervalu
hmotnost
malé části vlákna, pro kterou parametr nabývá hodnot z intervalu ![]() . Pak
lineární hustotou vlákna v bodě odpovídajícím
hodnotě parametru t nazveme veličinu [2]
. Pak
lineární hustotou vlákna v bodě odpovídajícím
hodnotě parametru t nazveme veličinu [2]
![]() .
.
![]() Zadání
Zadání
Určete hmotnost m nekonečně tenkého vlákna se zadanou
lineární hustotou ![]() .
.
Řešení
Interval ![]() nejdříve
rozdělíme dostatečně jemným dělením a hustotu
nejdříve
rozdělíme dostatečně jemným dělením a hustotu ![]() považujeme
na každém takto získaném segmentu za konstantní. Pak ovšem můžeme psát [3]
považujeme
na každém takto získaném segmentu za konstantní. Pak ovšem můžeme psát [3]
![]() ,
,
kde ![]() ,
, ![]() i
i ![]() jsou obecně různá
čísla z i-tého dělicího intervalu. Podobně jako v úloze 3 nedospíváme
sice takto k „čistou“ Riemannově integrální sumě, opět lze však dokázat, že
platí
jsou obecně různá
čísla z i-tého dělicího intervalu. Podobně jako v úloze 3 nedospíváme
sice takto k „čistou“ Riemannově integrální sumě, opět lze však dokázat, že
platí
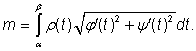
![]() Poznámka
Poznámka
Pro vlákno v prostoru s parametrizací ![]() ,
, ![]() a
a ![]() je možno odvodit
obdobný vzorec
je možno odvodit
obdobný vzorec
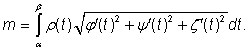
[1] Vlákno tedy v žádném bodě neprotíná samo sebe, nanejvýš může mít tvar uzavřené smyčky.
[2] Všimněte si, že ve jmenovateli uvedené
definiční rovnosti stojí přibližný výraz pro délku části vlákna na intervalu
![]() .
.
[3] S využitím Lagrangeovy věty o přírůstku.