6.7.2 Délka oblouku grafu funkce

Zadání

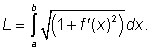Určete délku  L  oblouku grafu funkce    na intervalu  .

Řešení

Interval   rozdělíme dostatečně jemným dělením  a elementy grafu funkce  na každém z dělicích intervalů  nahradíme s přibližnou platností úsečkami o koncových bodech  a . Hledanou délku oblouku  L  pak získáme přibližně jako součet délek jednotlivých elementárních úseček , kde    a  . Platí tedy

,

kde jsme užili Lagrangeovu větu o přírůstku[1] a kde . Výsledkem našeho přibližného výpočtu je opět jistá Riemannova suma, které tentokrát odpovídá integrál  . Můžeme proto psát


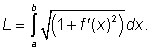
[1] Tato věta říká, že je-li funkce f(x) spojitá na intervalu    a diferencovatelná na  , pak existuje   takové, že  . Podrobnosti může čtenář najít v každé učebnici diferenciálního počtu (viz například Havlíček [1] nebo Jarník [3]).