6.7.1 Plocha pod grafem funkce

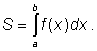Zadání

Určete plošný obsah  S  oblasti vymezené na intervalu    grafem funkce   a přímkami  ,    a  .[1]

Řešení

Budiž   dostatečně jemné dělení intervalu  .  Elementární plochy pod grafem funkce    nahradíme na každém z dělicích intervalů   obdélníky o stranách   a  ,  kde  . Hledaný plošný obsah  S  je pak dán s přibližnou platností jako součet plošných obsahů jednotlivých elementárních obdélníků :

.

Na pravé straně poslední rovnosti jsme ale takto získali Riemannovu integrální sumu, které při splnění nezbytných předpokladů (viz kapitola 3.6) odpovídá integrál   Můžeme proto psát

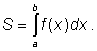
[1] Samostatně se pokuste zformulovat řešení podobné úlohy, v níž ale budeme předpokládat, že f(x) < 0, nebo dokonce že funkce  f  mění na intervalu  znaménko.