![]() 6.6.4 Numerický výpočet určitých integrálů
6.6.4 Numerický výpočet určitých integrálů
Mnoho funkcí, s nimiž se setkáváme v přírodovědných a technických aplikacích, nelze integrovat jednoduchými analytickými metodami. Při výpočtu takových integrálů se obvykle uchylujeme k numerickým metodám. Ústřední myšlenka numerického přístupu spočívá v náhradě integrované funkce funkcí jinou, zpravidla mnohem jednodušší, kterou již integrovat umíme. Přibližnou náhradou se pochopitelně dopouštíme chyby, kterou však většinou umíme učinit zanedbatelně malou.
Numerické integraci je věnováno významné místo v matematické
literatuře. V této kapitole zmíníme jen tři základní metody (obdélníkovou,
lichoběžníkovou a Simpsonovu) a omezíme
se při tom na výpočet vlastního integrálu ![]() , kde a
i b jsou reálná čísla. Zájemce o hlubší proniknutí do problematiky
odkazujeme na specializovanou literaturu (viz např. [4] a [5]).
, kde a
i b jsou reálná čísla. Zájemce o hlubší proniknutí do problematiky
odkazujeme na specializovanou literaturu (viz např. [4] a [5]).
Interval ![]() rozdělíme na
n stejných dílků s dělicími body
rozdělíme na
n stejných dílků s dělicími body
![]() ,
,
kde pro ![]()
![]() .
.
Na každém z dělicích intervalů ![]() ,
, ![]() , nahradíme funkci
f funkcí konstantní,
, nahradíme funkci
f funkcí konstantní, ![]() . Obvykle se používá
některá z následujících možností
. Obvykle se používá
některá z následujících možností
|
|
|
Novou, po částech konstantní funkci pak již snadno integrujeme a dostáváme
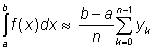 .
.
I zde, stejně jako v případě metody obdélníkové, rozdělíme
nejdříve interval ![]() na n
stejných dílků. Na každém z dělicích intervalů
na n
stejných dílků. Na každém z dělicích intervalů ![]() nahradíme integrovanou
funkci funkcí lineární, jejíž graf prochází body
nahradíme integrovanou
funkci funkcí lineární, jejíž graf prochází body ![]() a
a ![]() . Novou, nyní po
částech lineární funkci opět snadno integrujeme a dostáváme
. Novou, nyní po
částech lineární funkci opět snadno integrujeme a dostáváme
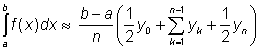 .
.
Interval ![]() rozdělíme v tomto
případě na sudý počet stejných dílků a na intervalech
rozdělíme v tomto
případě na sudý počet stejných dílků a na intervalech ![]() ,
, ![]() , ... a
, ... a ![]() nahradíme tentokrát
původní funkci f funkcemi kvadratickými, jejichž grafy procházejí na
prvním intervalu body
nahradíme tentokrát
původní funkci f funkcemi kvadratickými, jejichž grafy procházejí na
prvním intervalu body ![]() ,
, ![]() a
a
![]() , na
druhém intervalu body
, na
druhém intervalu body ![]() ,
, ![]() a
a
![]() atd. Novou,
v tomto případě po částech kvadratickou funkci integrujeme a dostáváme
atd. Novou,
v tomto případě po částech kvadratickou funkci integrujeme a dostáváme
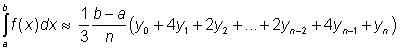 .
.
![]() Poznámka
Poznámka
Pro každou z uvedených metod získáváme zpravidla tím
přesnější výsledek, čím je dělení intervalu ![]() jemnější, a tedy
počet dělicích bodů větší. I přesnost uvedených metod roste obvykle při stejném
n v pořadí, v němž jsou uvedeny. Nejméně přesná je metoda
obdélníková, nejpřesnější metoda Simpsonova.
jemnější, a tedy
počet dělicích bodů větší. I přesnost uvedených metod roste obvykle při stejném
n v pořadí, v němž jsou uvedeny. Nejméně přesná je metoda
obdélníková, nejpřesnější metoda Simpsonova.