6.6.3 Nevlastní integrály

V předcházející kapitole jsme se naučili počítat určité Newtonovy a Riemannovy integrály na intervalech konečné délky. V aplikacích se však často vyskytne problém, kdy je třeba zadanou funkci integrovat přes interval, jehož jedna, či dokonce obě meze jsou nekonečné. V následujícím výkladu si ukážeme, jak se dá pojem určitého integrálu rozšířit i na intervaly nekonečné délky. V takovém případě pak obvykle hovoříme o integrálech nevlastních. V předcházející kapitole definované určité integrály pak, je-li to nutné v zájmu odlišení, nazýváme integrály vlastními.

Definice ("jednostranné" nevlastní integrály)

,
 .

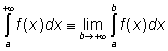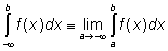Poznámka

Předpokládáme ovšem, že integrály i obě limity na pravé straně výše uvedených definičních rovností existují. Připouštíme přitom limity vlastní i nevlastní.

Máme-li navíc výše na mysli Newtonovy určité integrály, můžeme uvedené definiční rovnosti přepsat do tvaru [1]

,
.

Věta

Pro výše definované nevlastní integrály platí

,
,
,
.

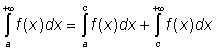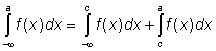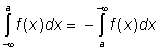Definice ("oboustranný" nevlastní integrál)

Dále definujeme

 ,

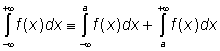kde  a  je libovolné reálné číslo.

Poznámka

Podle věty předcházející právě uvedené definici nezávisí pravá strana v této definici na volbě čísla  a.  Toto číslo je tedy skutečně libovolné.

Poznámka

Občas se setkáváme se situací, kdy primitivní funkce    existuje na celém otevřeném intervalu  , v samotných krajních bodech  a  a  b  však definována není, ač obě čísla mohou být konečná. Pak ovšem nelze použít definici Newtonova určitého integrálu v obvyklém tvaru

.

Inspirováni výkladem o nevlastních integrálech na nekonečných intervalech však snadno nahlédneme možnost, jak se s tímto problémem vypořádat. Stačí výše uvedenou definici přepsat do tvaru

,

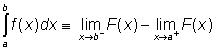který je již možno použít bez ohledu na to, zda jsou meze  a  a  b  konečné  či nikoliv a zda je v nich primitivní funkce    definována[2].  I v takovém případě hovoříme obvykle o nevlastním integrálu.

Pro konečné meze  a  a  b  a existující funkční hodnoty    a    přechází zobecněná definice (nevlastního) určitého integrálu na definici původní. Primitivní funkce je totiž v tomto případě na uzavřeném intervalu    spojitá, a platí tudíž    a  .