6.6.2 Riemannův určitý integrál

Definice (dělení intervalu)

Nechť  je uzavřený interval a čísla    splňují podmínku   . Pak uspořádanou množinu těchto čísel    nazveme dělením intervalu  .   Největší z čísel  ,  , nazveme normou dělení  D  a budeme pro ně užívat označení  .

Definice (Riemannova integrální suma)

Nechť    je dělení uzavřeného intervalu  ,    množina reálných čísel splňujících pro každé      a  f   omezená funkce na   [1].   Pak součet

nazveme Riemannovou integrální sumou funkce  f  pro dělení  D  a  množinu čísel  x.

Definice (Riemannův určitý integrál)

Nechť    je posloupnost dělení intervalu  ,  jejichž norma konverguje k nule, ,  a  x N  posloupnost množin čísel   z předcházející definice přiřazených dělením  .  Funkce    nechť je definována a omezená na intervalu  .  Existuje-li pro všechny takové posloupnosti jejich společná limita[2]

,

nazveme tuto limitu Riemannovým určitým integrálem funkce    na intervalu  [3].

Poznámka

Pro Riemannův určitý integrál budeme z důvodů, které objasníme níže, užívat stejné označení jako pro integrál Newtonův, tj. .

Poznámka

Podle předcházející definice umíme určit Riemannův integrál jen pro  .  Definujme proto dále

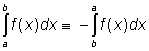  pro   ,

.

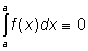Věta (o souvislosti Riemannova a Newtonova určitého integrálu)

Nechť je funkce   spojitá na uzavřeném intervalu  .  Pak existuje na tomto intervalu její Newtonův i Riemannův určitý integrál a oba jsou si rovny.

Poznámka

Předcházející věta ukazuje souvislost mezi Newtonovým a Riemannovým určitým integrálem pro jeden speciální typ funkcí - funkce spojité. Platí i obecnější tvrzení, že pokud pro danou funkci existují na intervalu    oba určité integrály (Newtonův i Riemannův), jsou si navzájem rovny. Proto se pro Newtonův a Riemannův integrál používá obvykle stejného označení. Důležitým důsledkem této věty je věta následující.

Věta

Funkce  f,  která je spojitá na  ,  má na    primitivní funkci. Pro pevně zvolené, leč libovolné    je    jednou z těchto primitivních funkcí.