6.6.1 Newtonův určitý integrál

Definice (Newtonův určitý integrál)

Nechť    je na intervalu  I  primitivní funkce k funkci  .  Newtonovým určitým integrálem funkce  f  od  a  do  b [1]  ()  nazveme číslo  .

Poznámka

Určitý integrál označujeme obvykle symbolem

,

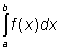kde číslo  b  nazýváme horní mezí  a číslo  a  dolní mezí tohoto integrálu.

Pro rozdíl funkčních hodnot primitivní funkce  F  v krajních bodech integračního oboru se často používá zápis

.

Poznámka

Všimněte si, že ačkoli primitivní funkce    není určena jednoznačně, určitý integrál   již jednoznačně určen je.

Věta

Funkce     je jednou z primitivních funkcí k funkci  [2]. Platí tedy

.

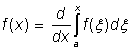Věta

Pro počítání s určitými Newtonovými integrály platí následující pravidla:

,
,
.

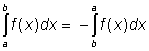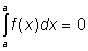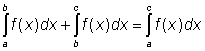Věta

Nechť pro každé  x  z intervalu    platí  .  Pak

.

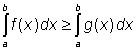Speciálně, je-li na intervalu    , můžeme psát

.

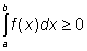Poznámka

Při výpočtu určitého Newtonova integrálu hledáme obvykle nejdříve primitivní funkci k zadané funkci Můžeme proto využít všech pravidel a vět, které jsou pro výpočet neurčitých integrálů (součtový vzorec, integrace per partes, substituce) formulovány v předcházejících kapitolách.

Někdy ale můžeme výsledek odhadnout přímo bez výpočtu primitivní funkce. Tak např.   je pro lichou funkci vždy nulový.