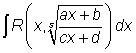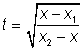6.5 Speciální substituce

Poměrně velké množství na první pohled komplikovaných integrálů je možno vhodně zvolenými substitucemi převést na integraci racionální lomené funkce, kterou jsme podrobně probrali v předcházející kapitole. Níže shrnujeme některé z těchto velmi užitečných a často používaných substitucí, jiné je možno nalézt ve všech pokročilých učebnicích a příručkách věnovaných integrálnímu počtu (viz např. [2], [4] a [5]).

Definice

Pod polynomem dvou proměnných    rozumíme konečný součet sčítanců typu  ,  kde p  a  q  jsou přirozená čísla nebo nula,

.

Pod racionální lomenou funkcí dvou proměnných     rozumíme podíl dvou polynomů dvou proměnných

.

Poznámka

Následující tabulka shrnuje některé speciální typy neurčitých integrálů, které je možno pomocí uvedených substitucí převést na integrály racionální lomené funkce.

Integrál

Omezující podmínky

Substituce

,
  [1]

,
  [2]

  [3]

,
 [4]


nebo
  [5]

 

,

 

 

Poznámka

Substituce v integrálu    podle návodu z výše uvedené tabulky vyžaduje provedení následujících náhrad [6]

,    a  .

Protože tato substituce vede velmi často k poměrně komplikovaným výrazům v integrandu počítaného integrálu, užívají se obvykle v níže uvedených speciálních případech substituce jiné:

·        platí-li [7] , je doporučována substituce  ,

·        platí-li ,  je výhodné použít substituce  ,

·        platí-li ,  položíme s výhodou  .



[1]  Je-li  ad - bc = 0,  je výraz pod odmocninou konstantní (dokažte) a úloha se mění na problém integrace prosté racionální lomené funkce.

[2]  V případě nulového či záporného diskriminantu kvadratického výrazu pod odmocninou je tento výraz definován v jediném bodě reálné osy či dokonce není definován vůbec.

[3] x1, x2 jsou kořeny kvadratického výrazu ax2 + bx + c.

[4]  Je-li diskriminant kvadratického výrazu pod odmocninou nulový, je možno provést naznačené odmocnění a úloha přechází na integraci racionální lomené funkce.

[5] Je-li ad - bc > 0,  můžeme též použít substituce  , kde   x1 a x2  jsou kořeny kvadratického polynomu pod odmocninou.

[6] Podrobnosti nalezne čtenář např. ve starší, leč vynikající základní učebnici Havlíčkově [2] nebo v pokročilé učebnici Jarníkově [4].

[7] pro všechna  x  a  y  z definičního oboru R