6.4.3 Integrace obecné racionální lomené funkce

Níže formulujeme obecná pravidla pro výpočet integrálů racionální lomené funkce

za předpokladu, že stupeň polynomu v čitateli je menší než stupeň polynomu ve jmenovateli [1], .

Pravidlo 1

Má-li polynom Qm(x) pouze jednoduché reálné kořeny, tj.

,

je výhodné integrovanou funkci psát ve tvaru [2]

,

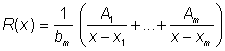kde neznámé reálné konstanty    nalezneme tak, že pravou stranu rovnosti převedeme na společného jmenovatele a takto získané koeficienty u jednotlivých mocnin  x  v čitateli porovnáme s odpovídajícími koeficienty polynomu . Výpočet integrálu    je pak převeden na výpočet integrálů z příkladu 1.

Pravidlo 2

Má-li polynom Qm(x) pouze reálné, obecně však násobné kořeny, tj. platí-li

,  ,

rozložíme integrovanou funkci do tvaru

,

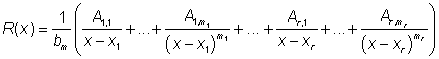kde neznámé reálné konstanty   nalezneme opět tak, že pravou stranu rovnosti převedeme na společného jmenovatele a takto získané koeficienty u jednotlivých mocnin  x  v čitateli porovnáme s odpovídajícími koeficienty polynomu  .  Výpočet integrálu    je takto převeden na výpočet integrálů z příkladů 1 a 2.

Pravidlo 3

Má-li polynom Qm(x) reálné i imaginární, obecně však násobné kořeny,  můžeme jej psát ve tvaru

,

kde uvedené kvadratické polynomy jsou již nerozložitelné. Pak je ovšem výhodné rozložit integrovanou funkci podle vzorce

,

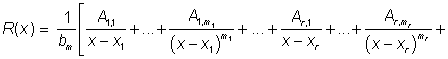
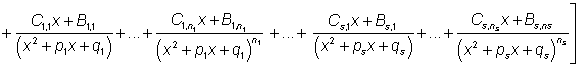kde reálné konstanty  Aij,  Bkl  a  Cpq  opět nalezneme tak, že pravou stranu rovnosti převedeme na společného jmenovatele a takto získané koeficienty u jednotlivých mocnin  x  porovnáme s odpovídajícími koeficienty polynomu  .  Výpočet integrálu    takto převádíme na výpočet integrálů z příkladů 1, 2, 3, 4 a 5.


[1] Protože obecná racionální lomená funkce může být vždy převedena dělením polynomů v čitateli a jmenovateli na součet polynomu a jiné racionální lomené funkce, která již uvedený předpoklad splňuje, je možno níže uvedených pravidel použít i ve zcela obecném případě.

[2] O rozkladech uvedených v pravidlech 1-3 se obvykle hovoří jako o rozkladech racionální lomené funkce na parciální zlomky.