Příklad (výpočet  pro ) [1]

Inspirováni postupem uvedeným v příkladu 4 můžeme okamžitě psát

.

Úloha je tedy převedena na výpočet dvou nových integrálů. První z nich počítáme podobně jako v  příkladě 4 pomocí první věty o substituci

.

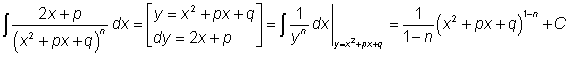Postup při výpočtu druhého integrálu závisí na tom, má-li kvadratický polynom ve jmenovateli reálné kořeny, či nikoliv:

·       pokud je má, a to navíc dva různé, musíme při výpočtu integrálu použít pravidlo 2 pro integrování obecné racionální lomené funkce (viz zde),
·        pokud je kořen kvadratického polynomu reálný a dvojnásobný, přechází počítaný integrál na integrál z příkladu 2.

Proveďme výpočet pro případ, kdy kvadratický výraz nemá reálné kořeny.

Podobně jako v příkladu 3c i nyní pomůže doplnění kvadratického trojčlenu na úplný čtverec. Také další postup je zcela obdobný tomu, který jsme nastínili v příkladu 3c:

.

Integrál   počítáme nejlépe pomocí rekurentního vzorce  (viz zde).