Příklad (výpočet , dva jednoduché reálné kořeny    a  )

.

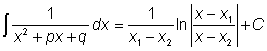Především můžeme psát , a počítaný integrál proto převést do tvaru

.

Dříve, než budeme pokračovat v integrování, upravíme racionální lomenou funkci do vhodnější podoby [1]

.

Neznámé konstanty  A  a  B  získáme převedením výrazu na pravé straně rovnosti na společného jmenovatele a porovnáním koeficientů u jednotlivých mocnin čitatele takto získaného zlomku s čitatelem levé strany rovnosti:

.

Odtud vyplývá

,

,

čili

  a  .

Nyní tedy můžeme psát

a podle výsledku příkladu 1 nakonec i

.