9.4.1 Obecná lineární diferenciální rovnice

Definice

Lineární diferenciální rovnicí -tého řádu rozumíme rovnici tvaru

,

kde tzv. koeficienty  a pravá strana  jsou funkcemi proměnné x.

Poznámka

·        Název je dán skutečností, že se na levé straně rovnice vyskytuje lineární výraz pro neznámou funkci  a pro její derivace.

·        Obecná lineární diferenciální rovnice je v obecném případě obtížně řešitelná. Níže jsou uvedeny základní teoretické poznatky, které budou užitečné v následující kapitole pro řešení speciálního typu této rovnice, tzv. lineární diferenciální rovnice s konstantními koeficienty.

Věta (o existenci a jednoznačnosti řešení)

Jestliže funkce  jsou spojité v intervalu I, pak existuje právě jedno řešení uvedené rovnice definované v celém intervalu I, které splňuje počáteční podmínku , , …, , kde  a , , …,  jsou libovolná reálná čísla.

Definice

Homogenní lineární diferenciální rovnicí příslušnou k původní rovnici, nazýváme rovnici

,

tj. rovnici bez pravé strany.

Věta

Libovolná lineární kombinace řešení homogenní lineární rovnice je také jejím řešením.

Důkaz

Přímým dosazením lineární kombinace řešení do rovnice a využitím linearity její levé strany a linearity operace derivace.

Definice (fundamentálního systému)

Systém , , …,  v intervalu I lineárně nezávislých řešení homogenní lineární rovnice se nazývá fundamentální systém této rovnice.

Věta

Tvoří-li funkce , , …,  fundamentální systém homogenní lineární rovnice, pak obecný integrál této rovnice má tvar

,

kde , , …,  jsou libovolné konstanty.

Věta

Známe-li fundamentální systém , , …,  homogenní rovnice, pak obecný integrál nehomogenní rovnice má tvar

,

kde , , …,  jsou libovolné konstanty a  je jakékoliv řešení (partikulární integrál) nehomogenní rovnice.

Důkaz

Stačí dosadit uvedené řešení do nehomogenní rovnice a opět využít její linearity.

Poznámka

·        Slovně řečeno, obecný integrál nehomogenní rovnice je součtem obecného integrálu rovnice homogenní a libovolného partikulárního integrálu rovnice nehomogenní.

·        O tom, jak najít partikulární integrál nehomogenní rovnice, hovoří následující věta.

Věta (metoda variace konstant)

Partikulární integrál  nehomogenní rovnice lze hledat ve tvaru

,

tj. ve tvaru obecného řešení homogenní rovnice, kde však veličiny , , …,  nepovažujeme za konstanty, ale za neznámé funkce proměnné x (tzv. metoda variace konstant). Dá se dokázat, že funkce  je hledaným řešením právě tehdy, vyhovují-li neznámé funkce , , …,  soustavě diferenciálních rovnic prvního řádu

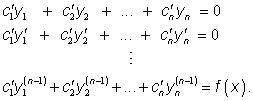
Tuto soustavu řešíme obdobným postupem jako algebraické soustavy lineárních rovnic (eliminační metodou, Cramerovým pravidlem apod.). Integrací získaných prvních derivací , , …,  nakonec dostaneme hledané funkce , , …,  a následně partikulární řešení .