9.2 Vybrané diferenciální rovnice prvního řádu
9.2.1 Rovnice typu

Za předpokladu, že funkce je ve vyšetřovaném oboru spojitá, má uvedená rovnice obecný integrál

.

Integrační konstanta je zahrnuta v neurčitém integrálu. Partikulární integrál vyhovující počáteční podmínce  je

.

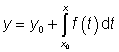Na pravé straně poslední rovnice se jedná o integrál jako funkci horní meze.

9.2.2 Rovnice typu

Za předpokladu, že funkce je ve vyšetřovaném oboru spojitá a různá od nuly, řešíme rovnici přepsáním na tvar , čímž uvedenou rovnici převedeme na rovnici předchozího typu pro funkci . Obecným integrálem je tudíž  a partikulárním integrálem .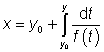

9.2.3 Rovnice separovatelná  

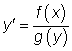
Věta

Je-li funkce  spojitá v intervalu  a funkce  spojitá a různá od nuly v intervalu , pak uvedená rovnice má v oblasti  obecný integrál

.

Partikulární integrál procházející bodem  je dán rovnicí

.

Poznámka

·        Tento typ diferenciální rovnice v sobě zahrnuje oba dva předchozí typy jako speciální případy.

·        Název této rovnice souvisí s tím, že ji řešíme tzv. separací proměnných, tj. jejich oddělením na jednotlivé strany rovnice.

9.2.4 Rovnice homogenní

Předpokládá se  ve vyšetřovaném oboru. Řešíme zavedením nové funkce  neboli . Derivováním poslední rovnice podle x dostaneme vztah . Dosadíme-li uvedené výrazy za  a  do původní rovnice, dostaneme diferenciální rovnici , kterou jednoduše upravíme na rovnici se separovanými proměnnými . Najdeme-li její řešení , je řešením původní rovnice funkce .

Poznámka

·        Termín homogenní v názvu rovnice znamená, že na pravé straně se jedná o tzv. homogenní funkci (nultého stupně). Připomeňme, že funkce  se nazývá  homogenní s-tého stupně, platí-li .

·        Na homogenní rovnici lze převést rovnici  tak, že se vhodnou substitucí ,  zbavíme absolutních členů , .

9.2.5 Rovnice lineární

Věta

Jsou-li funkce ,  spojité v určitém intervalu, existuje v tomto intervalu právě jedno řešení uvedené rovnice splňující danou počáteční podmínku.

Poznámka

Postup nalezení řešení je následující. Nejprve řešíme rovnici bez pravé strany, tzv. homogenní rovnici (nezaměňovat s názvem předchozí diferenciální rovnice!) . Tato rovnice se řeší separací proměnných:

.

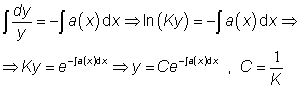Obecný integrál původní rovnice (nehomogenní, s pravou stranou) dostaneme tzv. metodou variace konstanty. Předpokládáme, že řešení nehomogenní rovnice má stejný tvar jako řešení homogenní rovnice, avšak integrační konstantu považujeme za funkci proměnné x:

.

Tento výraz derivujeme podle x a dosadíme do původní rovnice:

.

Dostaneme diferenciální rovnici se separovanými proměnnými pro funkci , jejímž řešením je

.

Dosazením do předpokládaného řešení nehomogenní rovnice obdržíme nakonec obecný integrál ve tvaru

.

9.2.6 Rovnice exaktní

Definice

Je dána rovnice 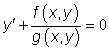, kde funkce ,  mají v určité oblasti  spojité derivace prvního řádu. Rovnici lze snadno převést na diferenciální formu . Pokud je levá strana poslední rovnice v  totálním diferenciálem nějaké funkce , jedná se o tzv. exaktní rovnici.

Věta

Obecný integrál exaktní rovnice je dán rovnicí  (význam symbolů viz v předchozí definici).

Poznámka

·        Aby výraz  byl totálním diferenciálem, musí v  platit rovnost .

·        Vlastní řešení probíhá tak, že nejprve ověříme, zda platí rovnost

,

a pokud ano, nalezneme funkci . Tato funkce je s funkcemi  a  svázána vztahy

 a ,

odkud

 a .

·        Pokud rovnice není exaktní, můžeme se pokusit najít takovou funkci , zvanou integrační faktor, aby rovnice  byla exaktní. Najít integrační faktor není obecně snadné, protože musíme řešit parciální diferenciální rovnici

.

Dá se však snadno ukázat, že pokud je výraz

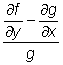, resp. ,

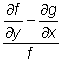funkcí pouze proměnné x, resp. y, je také integrační faktor funkcí pouze x, resp. y, a nalezneme jej řešením rovnice

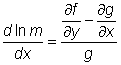, resp. .

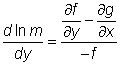9.2.7 Rovnice typu

Rovnici přepíšeme na tvar , kde jsme zavedli parametr . Derivací podle x a opětným dosazením parametru  za  obdržíme rovnici

 a po úpravě

.

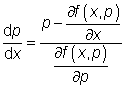Toto je rovnice prvního řádu pro neznámou funkci  rozřešená vzhledem k derivaci. Nalezneme-li její obecný integrál , dosazením do původní rovnice obdržíme její obecné řešení .

Poznámka

·        Jedná se o rovnici nerozřešenou vzhledem k první derivaci.

·        Lze také nejprve derivovat výchozí rovnici podle , čímž dostaneme rovnici druhého řádu

,

ve které nevystupuje , a teprve do této rovnice dosadit  za , čímž dosáhneme snížení jejího řádu.

·        Zajímavý moment nastává v okamžiku, kdy již máme řešení . Místo dosazení do původní rovnice se nabízí také možnost vrátit se k  a řešit úlohu . Tím bychom však dostali řešení rovnice druhého řádu uvedené v předchozím bodě této poznámky (se dvěma integračními konstantami), což není naším úkolem.

·        Speciálním případem je rovnice  zvaná Clairautova (čteme „klerotova“). Výše uvedeným postupem snadno zjistíme, že její obecné řešení má tvar

,

a navíc objevíme, že existuje i další, singulární řešení, které vyhovuje rovnici

.

9.2.8 Rovnice typu

Tuto rovnici řešíme obdobně jako předchozí typ. Zavedením parametru a derivací rovnice podle  (pozor, ne podle ) obdržíme rovnici prvního řádu

pro neznámou funkci , kterou opět můžeme jednoduše převést na rovnici

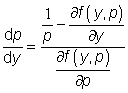
rozřešenou vzhledem k první derivaci. Obecný integrál této rovnice  dosadíme do výchozí rovnice a obdržíme její obecný integrál v implicitním tvaru

.

Poznámka

·        Jedná se o rovnici nerozřešenou vzhledem k první derivaci.

·        Stejným způsobem je možné řešit rovnice  , resp. , které jsou speciálními případy obou předchozích typů.