8.8 Vyjádření diferenciálních operátorů v křivočarých
souřadnicích Níže shrnujeme základní vzorce nezbytné pro použití nejdůležitějších vektorových diferenciálních operátorů (gradient, divergence, rotace a Laplaceův operátor) ve vybraných křivočarých souřadnicových soustavách[1]. Podrobnosti může čtenář nalézt např. v příručce Rektorysově [5].
8.8.1 Polární souřadnice v rovině
Označme vektory lokální křivočaré báze polárních souřadnic symboly er
a ej. Dále nechť f je diferencovatelná
funkce, 
, a A
diferencovatelné vektorové pole, 
, které rozkládáme
v každém bodě roviny do lokální křivočaré báze 
.
Pak platí
,
,
.
8.8.2 Válcové souřadnice v prostoru
Vektory lokální křivočaré báze válcových souřadnic označme symboly er,
ej
a ez. Podobně jako výše nechť je f
diferencovatelná funkce, 
, a A
diferencovatelné vektorové pole, 
. I nyní toto
pole rozkládáme v každém bodě prostoru do lokální křivočaré báze: 
.
Pak platí
,
,
,
.
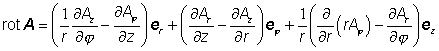8.8.3 Kulové souřadnice v prostoru
Označme i nyní vektory lokální křivočaré báze er,
ej
a eq. Dále nechť f je opět diferencovatelná
funkce, 
, a A
diferencovatelné vektorové pole, 
, jehož rozklad
do lokální křivočaré báze je dán jako 
.
Pak platí
,
,
,
.
8.8.4 Obecné ortogonální souřadnice
Jednotkové vektory lokální křivočaré ortogonální[2] báze válcových souřadnic označme symboly e1,
e2 a e3. Podobně
jako výše nechť je f diferencovatelná funkce, 
, a A
diferencovatelné vektorové pole, 
. Toto pole rozkládáme
v každém bodě prostoru do lokální křivočaré ortogonální báze: 
. Infinitezimálně
malé posunutí 
můžeme obecně
vyjádřit ve tvaru 
, kde veličiny
, 
, 
jsou obecně funkcemi
souřadnic 
, 
, 
a nazývají se
Laméovy koeficienty.
Pak platí[3]
,
,
,
.
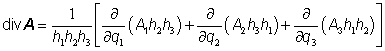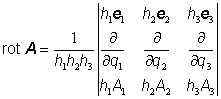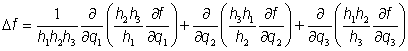[1]
Viz též apendix A5.
[2] Odtud
název „ortogonální souřadnice“. Blíže o ortogonálních bázích viz kap. A4.1
a o ortogonálních souřadnicích viz kap. A5.
[3] Ve výrazu
pro rotaci svislé čáry označují determinant – viz kap. A4.3.