8.4 Rotace
Definice
Rotací vektorového pole 
nazýváme vektorové
pole
.
Poznámka
·
Stačí si zapamatovat pouze tvar první složky, ostatní složky
dostaneme cyklickou záměnou indexů a proměnných.
·
Tuto definici není možné zobecnit na případ jiného počtu proměnných
než tři.
·
Pomocí nabla operátoru lze zapsat divergenci jako symbolický
vektorový součin 
.
Příklad
Snadno lze podle definice spočítat, že rotací vektorového pole 
, tj. pole polohového
vektoru, je nulové vektorové pole: 
.
Poznámka
Na základě Stokesovy věty integrálního počtu (viz kapitola 5.8) můžeme pro rotaci psát vyjádření
.
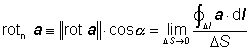Plocha 
je orientovaná
rovinná plocha obsahující zvolený bod a ohraničená kladně orientovanou křivkou
, úhel 
je úhel mezi vektorem
a normálou k ploše
. Vzorec je třeba
chápat tak, že hodnota kolmé složky divergence k infinitezimální rovinné
plošce 
(jejíž poloha
je určena jejím normálovým vektorem) je dána podílem cirkulace vektoru 
po ohraničující
křivce 
a velikosti plochy
. Jinak řečeno,
směr a orientace vektoru 
ve zvoleném bodě
odpovídají směru a orientaci normály k jednotkové (dostatečně malé) plošce
, jejíž poloha
(sklon) maximalizuje cirkulaci vektoru 
po její hraniční
křivce (tj. veličinu 
). Velikost vektoru
je dána maximální
hodnotou uvedené cirkulace.
Poznámka
V modelu proudící kapaliny (viz divergence) vektor 
určuje směr osy,
kolem které se kapalina v okolí uvažovaného bodu otáčí, a jeho velikost
je rovna dvojnásobku rychlosti otáčení (v obloukové míře).
Definice
Body, ve kterých je 
, označujeme jako
víry. Pole, pro které platí identicky (tj. v každém
jeho bodě) 
, se nazývá nevírové
pole. Pole, v jehož alespoň jednom bodě je 
, nazýváme vírovým
polem.
Věta
Pro rotaci platí:
,
,
.
