![]() Definice
Definice
Tzv. Hamiltonův
operátor nabla (nabla operátor) je symbolický
operátor, který se značí ![]() a zavádí se takto:
a zavádí se takto:
![]() .
.
Formálně se jedná o vektor, jehož složkami jsou symboly parciálních derivací podle kartézských souřadnic x, y, z.
![]() Poznámka
Poznámka
Nejedná se o operátor v pravém slova smyslu, neboť není dán předpis, jak tento operátor aplikovat ani jeho definiční obor. V tom je ale právě jeho přednost, protože se ukazuje, že pomocí nabla operátoru se dají elegantně vyjádřit všechny dříve uvedené diferenciální operátory.
![]() Věta (vyjádření operátorů pomocí operátoru
nabla)
Věta (vyjádření operátorů pomocí operátoru
nabla)
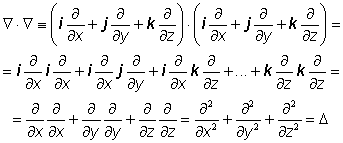 .
.