8.3 Divergence 
Definice
Divergencí vektorového pole 
nazýváme skalární
pole
.
Poznámka
·
Slovně řečeno, jedná se o součet tří parciálních derivací, kde
první člen je derivací první složky vektorového pole podle první proměnné,
druhý člen derivací druhé složky podle druhé proměnné a třetí člen derivací
třetí složky podle třetí proměnné. V každém sčítanci tudíž index složky
odpovídá pořadí (indexu) proměnné.
·
Definici lze snadno zobecnit pro případ 
proměnných.
·
Pomocí nabla operátoru lze zapsat divergenci jako symbolický
skalární součin 
.
Příklad
Snadno lze podle definice spočítat, že divergencí skalárního pole 
tj. pole velikostí
polohového vektoru 
, je konstantní
skalární pole: 
.
Poznámka
Na základě Gaussovy věty integrálního počtu (viz kapitola 5.8) můžeme pro divergenci psát vyjádření
.
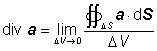Plocha 
je kladně orientovaná
uzavřená plocha ohraničující objem 
, který obsahuje
zvolený bod. Hodnota divergence v určitém bodě představuje tok vektoru
z infinitezimálního
objemu 
dělený tímto objemem
neboli tok vektoru 
z jednotkového
objemu v daném bodě.
Poznámka
Jednoduchý
fyzikální model. Jestliže vektorové pole 
charakterizuje
rychlost proudění kapaliny, pak 
v určitém
bodě udává objemové množství kapaliny, které vyteče z jednotkového objemu
za jednotku času, tzn. vydatnost tohoto jednotkového objemu jakožto zřídla
kapaliny.
Definice
Pole, pro které platí identicky (tj. v každém jeho bodě) 
, se nazývá nezřídlové
pole. Jestliže alespoň v jednom bodě platí 
, pak pole 
nazýváme zřídlovým.
Věta
Pro divergenci platí:
, 
.
Důkaz
Důkaz je triviální, plyne z vět pro derivaci součtu a součinu funkcí.