Soustavy lineárních rovnic, matice, determinanty
Začneme maticemi a determinanty, abychom s jejich pomocí mohli elegantně
formulovat řešení soustavy lineárních rovnic.
- Matice – základní pojmy
Maticí A
typu (m, n) nazýváme schéma mn čísel (reálných nebo i komplexních)
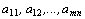 , sestavených
v m řádcích a n sloupcích:
, sestavených
v m řádcích a n sloupcích:
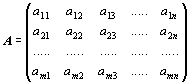 .
.
První index v označení
prvku je tedy řádkový, druhý sloupcový. Často používaný zkrácený zápis (pokud
víme, o jaký typ matice se jedná, je 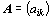 .
Prvky
.
Prvky 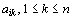 pro
dané i tvoří i-tý řádek, prvky
pro
dané i tvoří i-tý řádek, prvky 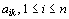 pro dané k tvoří k-tý sloupec. Řádky a sloupce se souhrnně
nazývají řady.
pro dané k tvoří k-tý sloupec. Řádky a sloupce se souhrnně
nazývají řady.
Je-li m=n, pak
se A nazývá čtvercovou maticí m-tého stupně (m-tého řádu),
jinak se jedná o matici obdélníkovou.
Prvky 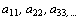 tvoří
hlavní diagonálu a nazývají se hlavní prvky, prvky
tvoří
hlavní diagonálu a nazývají se hlavní prvky, prvky 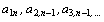 tvoří
vedlejší diagonálu.
tvoří
vedlejší diagonálu.
Nulovou maticí
nazýváme matici, jejíž všechny prvky se rovnají nule. Značíme obvykle symbolem
0 nebo číselnou nulou (0).
Diagonální maticí
nazýváme čtvercovou matici, u které prvky na hlavní diagonále jsou různé od
nuly a ostatní prvky rovny nule.
Jednotkovou maticí
nazýváme takovou diagonální matici, jejíž všechny hlavní prvky jsou rovny
1. Jednotková matice se obvykle značí E, I nebo
i číslem 1.
Horní (také
pravou) trojúhelníkovou maticí nazýváme čtvercovou matici 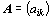 ,
jestliže pod hlavní diagonálou jsou všechny prvky nulové, tzn.
,
jestliže pod hlavní diagonálou jsou všechny prvky nulové, tzn. 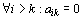 .
.
Dolní (také
levou) trojúhelníkovou maticí nazýváme čtvercovou matici 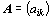 ,
jestliže nad hlavní diagonálou jsou všechny prvky nulové, tzn.
,
jestliže nad hlavní diagonálou jsou všechny prvky nulové, tzn. 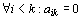 .
.
- Hodnost matice a elementární úpravy
Hodností 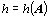 matice A typu
matice A typu 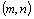 nazýváme maximální počet lineárně nezávislých řádků, který je roven maximálnímu
počtu lineárně nezávislých sloupců matice A. Má-li tedy např.
matice A 5 lineárně nezávislých řádků, pak její hodnost je rovna
5. Z definice zřejmě plyne
nazýváme maximální počet lineárně nezávislých řádků, který je roven maximálnímu
počtu lineárně nezávislých sloupců matice A. Má-li tedy např.
matice A 5 lineárně nezávislých řádků, pak její hodnost je rovna
5. Z definice zřejmě plyne 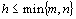 .
.
Elementárními úpravami
matice A rozumíme takové úpravy, které nemění její hodnost. Jsou
to:
- Přehození pořadí řad.
- Vynásobení některé řady
číslem různým od nuly.
- Přidání k matici
A řady, která je lineární kombinací ostatních řad matice A.
- Vynechání v matici
A řady, která je lineární kombinací ostatních řad matice A.
- Přičtení k některé
řadě matice A lineární kombinace ostatních řad.
O matici B,
která je stejného typu jako matice A, a vznikla z matice
A elementárními úpravami, říkáme, že je ekvivalentní s maticí
A. Zapisujeme A~B. Ekvivalentní matice mají tedy stejnou
hodnost.
- Operace s maticemi
Rovnost matic.
Matice 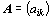 se
rovná matici
se
rovná matici 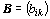 právě tehdy, jsou-li obě matice stejného typu a jejich stejnolehlé prvky se
rovnají. Jiný zápis:
právě tehdy, jsou-li obě matice stejného typu a jejich stejnolehlé prvky se
rovnají. Jiný zápis: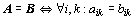 .
.
Součet dvou matic.
Matice C je součtem matic A, B právě
tehdy, jsou-li všechny tři matice téhož typu a platí, že každý prvek matice
C je součtem stejnolehlých prvků matic A, B.
Jiný zápis: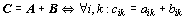 .
Je zřejmé, že pro sčítání matic platí asociativní a komutativní zákon:
.
Je zřejmé, že pro sčítání matic platí asociativní a komutativní zákon:
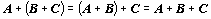 ,
,
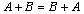 .
.
Násobení matice číslem.
Součinem matice 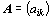 a čísla
a čísla 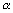 je
matice
je
matice 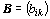 stejného
typu jako matice A, pro jejíž prvky platí
stejného
typu jako matice A, pro jejíž prvky platí 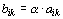 .
Jiný zápis:
.
Jiný zápis: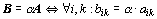
Pro násobení matice číslem platí distributivní zákony a asociativní zákon:
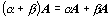 ,
, 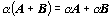 ,
,
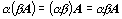 .
.
Násobení matic.
Součinem matice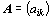 typu
typu 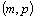 a matice
a matice
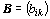 typu
typu 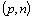 nazýváme matici
nazýváme matici 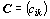 typu
typu 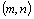 , kterou
označujeme
, kterou
označujeme 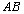 (nebo s tečkou
(nebo s tečkou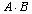 )
a pro jejíž prvky platí:
)
a pro jejíž prvky platí: 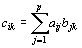 .
.
Poznámka:
- Součin matic je tedy
definován pouze tehdy, je-li počet sloupců první (levé) matice roven počtu
řádků (druhé) pravé matice.
- Prvek
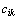 součinu
součinu 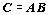 je vlastně skalárním součinem i-tého řádku matice A a
k-tého sloupce matice B.
je vlastně skalárním součinem i-tého řádku matice A a
k-tého sloupce matice B.
- Násobkem čtvercové
matice A a jednotkové matice E (téhož typu) je
původní matice A:
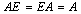 .
.
- Máme-li součin
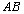 , říkáme,
že matice A násobí matici B zleva, nebo také že
matice B násobí matici A zprava. Obecně totiž
neplatí komutativní zákon, tzn. pro většinu matic
, říkáme,
že matice A násobí matici B zleva, nebo také že
matice B násobí matici A zprava. Obecně totiž
neplatí komutativní zákon, tzn. pro většinu matic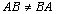 .
.
- Pro násobení matic platí
distributivní zákony a asociativní zákon:
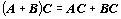 ,
, 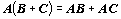 ,
,
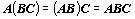
.
Inverzní maticí
k čtvercové matici A nazýváme takovou matici (pokud existuje)
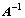 stejného typu,
pro kterou platí
stejného typu,
pro kterou platí 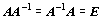 ,
kde E je jednotková matice (téhož typu). Inverzní matice k matici
A řádu n existuje právě tehdy, je-li hodnost čtvercové
matice A rovna jejímu řádu n, tj.
,
kde E je jednotková matice (téhož typu). Inverzní matice k matici
A řádu n existuje právě tehdy, je-li hodnost čtvercové
matice A rovna jejímu řádu n, tj. 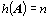 .
Taková matice se nazývá regulární; pokud
.
Taková matice se nazývá regulární; pokud 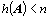 ,
hovoříme o matici singulární.
,
hovoříme o matici singulární.
K výpočtu inverzní
matice se nejčastěji používá Gaussovy metody inverze matic. Tato metoda
je založena na tom, že k inverzní matici lze přejít pomocí pouze řádkových,
příp. sloupcových elementárních úprav, přičemž nejprve dostaneme jednotkovou
matici, a pak aplikací týchž elementárních úprav ve stejném pořadí přejdeme
k inverzní matici.
Mocniny matic.
Pro čtvercovou regulární matici A definujeme celočíselnou mocninu
takto (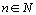 ):
):
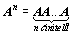 ,
tzn. jako opakované násobení n stejných matic .
,
tzn. jako opakované násobení n stejných matic .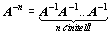 ,
tzn. jako opakované násobení n inverzních matic .
,
tzn. jako opakované násobení n inverzních matic .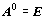 .
.
Platí obdobná věta jako
pro číselné mocniny: 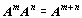 ,
,
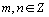 .
.
Transponovanou maticí
k matici A typu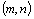 nazýváme matici
nazýváme matici 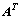 typu
typu 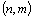 takovou,
kterou dostaneme z matice A záměnou (transpozicí) řádků a sloupců. Označíme-li
prvek v i-tém řádku a k-tém sloupci transponované matice
takovou,
kterou dostaneme z matice A záměnou (transpozicí) řádků a sloupců. Označíme-li
prvek v i-tém řádku a k-tém sloupci transponované matice
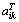 , pak můžeme
psát:
, pak můžeme
psát: 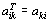 . Jinak
řečeno, transponovaná matice
. Jinak
řečeno, transponovaná matice 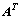 vznikne překlopením matice A kolem její hlavní diagonály.
vznikne překlopením matice A kolem její hlavní diagonály.
Platí: 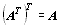 ,
, 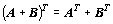 ,
,
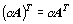 ,
, 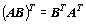 ,
,
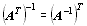 .
.
Pokud pro čtvercovou
matici A platí rovnost 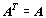 ,
hovoříme o souměrné (symetrické) matici. Pro její prvky tedy platí
,
hovoříme o souměrné (symetrické) matici. Pro její prvky tedy platí
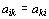 .
.
- Determinant
Determinantem čtvercové
matice 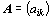 řádu n nazýváme číslo
řádu n nazýváme číslo 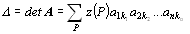 ,
kde sčítáme přes všechny permutace P množiny
,
kde sčítáme přes všechny permutace P množiny 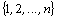 a
a 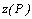 je znaménko
permutace P.
je znaménko
permutace P.
Poznámka:
- Znaménko permutace
P je dáno vztahem
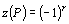 ,
kde r je počet tzv. inverzí v permutaci P. Inverzí
v permutaci
,
kde r je počet tzv. inverzí v permutaci P. Inverzí
v permutaci 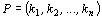 nazýváme každou dvojici
nazýváme každou dvojici 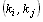 ,
pro kterou platí
,
pro kterou platí 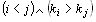 .
Pokud je číslo r sudé, hovoříme o sudé permutaci a její znaménko
je rovno 1, pokud je r liché, jedná se o lichou permutaci a
její znaménko je rovno –1. Tak např. permutace
.
Pokud je číslo r sudé, hovoříme o sudé permutaci a její znaménko
je rovno 1, pokud je r liché, jedná se o lichou permutaci a
její znaménko je rovno –1. Tak např. permutace 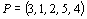 je lichá, protože obsahuje 3 inverze:
je lichá, protože obsahuje 3 inverze: 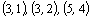 .
.
- Kromě uvedeného značení
pomocí symbolu
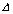 nebo
nebo 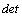 se
používá také stejný zápis jako u matic, ale místo kulatých závorek se píší
svislé čáry jako u absolutní hodnoty.
se
používá také stejný zápis jako u matic, ale místo kulatých závorek se píší
svislé čáry jako u absolutní hodnoty.
- Sčítance
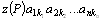 se nazývají členy determinantu. Z definice determinantu je zřejmé, že
každý člen determinantu
se nazývají členy determinantu. Z definice determinantu je zřejmé, že
každý člen determinantu 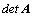
je součin n prvků
matice A (a znaménka příslušné permutace), přičemž z každého
řádku a sloupce matice A obsahuje právě jeden prvek. Nemohou se
v něm tudíž vyskytovat dva prvky ze stejného řádku nebo sloupce.
Subdeterminantem (minorem)
k-tého řádu matice A typu 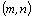 nazýváme determinant takové matice, která vznikne z matice A
vypuštěním tolika řádků a sloupců, aby z ní zbyla čtvercová matice k-tého
řádu.
nazýváme determinant takové matice, která vznikne z matice A
vypuštěním tolika řádků a sloupců, aby z ní zbyla čtvercová matice k-tého
řádu.
Vypočítat determinant
matice prvního řádu je triviální: 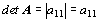 (pozor, nejedná se o absolutní hodnotu, ale označení determinantu), výsledkem
je tedy hodnota jediného prvku této matice.
(pozor, nejedná se o absolutní hodnotu, ale označení determinantu), výsledkem
je tedy hodnota jediného prvku této matice.
Výpočet determinantu
matice druhého řádu je také velmi snadný: 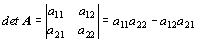 .
.
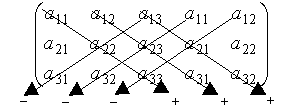
Výpočet determinantu matice
třetího řádu je již méně příjemný, protože bude mít 6 členů (=3!) a hůře se
také zjišťuje znaménko každého členu. Používá se proto schéma zvané Sarrusovo
pravidlo: K matici A připíšeme první dva sloupce (obdobně
je možné formulovat toto pravidlo pro řádky, to zde nebudeme dělat) a pak provádíme
součiny po přímých čárách tak, jak je naznačeno na schématu, přičemž jde-li
čára ve směru zleva doprava, je znaménko kladné, v opačném případě záporné.
Pro výpočty determinantů matic čtvrtého a vyšších řádů není vhodné postupovat
přímo podle definice, protože počet členů je příliš velký a výpočet zbytečně
zdlouhavý. Proto se používá jiných metod, založených na následujících větách:
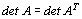 .
.- Zaměníme-li v matici
navzájem dvě rovnoběžné řady, změní determinant znaménko.
- Společného nenulového
činitele jedné řady lze vytknout před determinant.
- Determinant je roven
nule právě tehdy, jestliže prvky alespoň jedné řady jsou rovny nule nebo jestliže
nějaká řada je lineární kombinací řad s ní rovnoběžných.
- Determinant se nezmění,
přičteme-li k libovolné řadě jakoukoliv lineární kombinaci ostatních
řad s ní rovnoběžných.
- Rozvoj determinantu
podle prvků jedné řady:
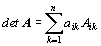 (rozvoj
podle i-tého řádku), resp.
(rozvoj
podle i-tého řádku), resp. 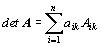 (rozvoj podle k-tého sloupce),
(rozvoj podle k-tého sloupce),
kde číslo 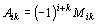 je tzv. algebraický doplněk prvku
je tzv. algebraický doplněk prvku 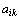 a
a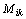
je subdeterminant, vzniklý
z matice A vynecháním i-tého řádku a k-tého sloupce.
Vidíme, že tato věta převádí výpočet determinantu n-tého řádu na výpočet
n determinantů (n-1)-ho řádu. Je proto výhodné před výpočtem determinantu
rozvojem podle prvků vybrané řady provést takové úpravy matice, které nezmění
hodnotu determinantu a vynulují ve vybrané řadě co nejvíce prvků. Tím odpadne
potřeba příslušné subdeterminanty počítat. Konkrétně je velmi výhodné převést
matici na trojúhelníkovou (horní nebo dolní). Pak je determinant roven součinu
hlavních prvků.
Poznámka:
Z věty ad 4) plyne,
že determinant regulární matice je různý od nuly. Máme tedy tři ekvivalentní
vyjádření pro regulární matici: matice A typu 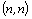 je
regulární
je
regulární 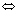
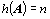
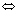
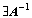
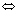
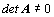 .
.
- Řešení soustav lineárních rovnic
Soustavou n lineárních
rovnic o n neznámých rozumíme tuto soustavu rovnic:
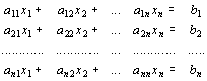
Ze střední školy umíme takové soustavy řešit buď dosazovací metodou, sčítací
metodou nebo Gaussovou eliminační metodou. My se zaměříme na řešení pomocí maticového
počtu, přičemž se podíváme také na exaktní formulaci podmínek, za kterých uvedená
soustava má řešení, příp. kolik má řešení.
Matici 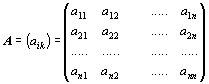 typu
typu 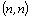 nazveme
maticí soustavy, matici
nazveme
maticí soustavy, matici  typu
typu 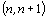 , která
vznikne z matice A přidáním sloupce pravých stran, nazveme
rozšířenou maticí soustavy. Dále označme sloupcovou matici
, která
vznikne z matice A přidáním sloupce pravých stran, nazveme
rozšířenou maticí soustavy. Dále označme sloupcovou matici 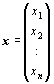 ,
resp.
,
resp. 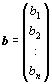 jako
vektor neznámých, resp. vektor pravých stran. Pak původní soustavu
můžeme zapsat v maticovém tvaru
jako
vektor neznámých, resp. vektor pravých stran. Pak původní soustavu
můžeme zapsat v maticovém tvaru 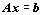 .
.
Podmínky řešitelnosti
soustavy lineárních rovnic řeší následující věta:
Soustava lineárních rovnic
je řešitelná právě tehdy, má-li matice soustavy a rozšířená matice soustavy
stejnou hodnost h. Pro 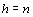 existuje právě jedno řešení, pro
existuje právě jedno řešení, pro 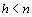 existuje řešení nekonečně mnoho.
existuje řešení nekonečně mnoho.
Poznámka:
- Žádné řešení, tzn.
případ, kdy hodnost matice soustavy se nerovná hodnosti rozšířené matice soustavy,
nastane tehdy, když si rovnice vzájemně odporují, např. je-li levá strana
nějaké rovnice lineární kombinací levých stran ostatních rovnic, ale její
pravá strana není stejnou lineární kombinací pravých stran příslušných
rovnic.
- Nekonečně mnoho řešení,
tzn. případ, kdy hodnost matice soustavy se rovná hodnosti rozšířené matice
soustavy, ale je menší než n, nastane tehdy, když nějaká rovnice je
již “obsažena” v ostatních rovnicích, např. je jejich lineární kombinací.
Pak počet proměnných převyšuje počet nezávislých rovnic a je možné alespoň
jednu proměnnou zvolit za parametr.
- Z uvedeného plyne, že právě jedno řešení má soustava tehdy a jen tehdy,
je-li matice soustavy regulární.
- V případě homogenní
soustavy (tj. soustavy, kdy vektor pravých stran b je nulovou
maticí, tzn.
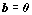
) existuje řešení vždy, protože
přidáním nulové řady k matici se její hodnost nezmění.
Konkrétní tvar řešení
udává tzv. Cramerovo pravidlo:
Jestliže determinant
matice soustavy je různý od nuly 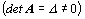 ,
pak má soustava právě jedno řešení
,
pak má soustava právě jedno řešení 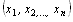 ,
kde
,
kde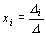 , přičemž
, přičemž
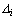 je determinant
matice Ai, která vznikne z matice soustavy
A tak, že v ní i-tý sloupec nahradíme sloupcem pravých
stran.
je determinant
matice Ai, která vznikne z matice soustavy
A tak, že v ní i-tý sloupec nahradíme sloupcem pravých
stran.
Poznámka:
Cramerovo pravidlo se
nehodí k praktickému řešení soustav lineárních rovnic, protože počítat
determinanty je obecně dosti pracné. Má svůj význam především teorii, protože
nám explicitně ukazuje tvar řešení. Nejpoužívanější metodou pro řešení soustav
lineárních rovnic je Gaussova eliminační metoda, která v maticové formulaci
znamená v podstatě převod rozšířené matice soustavy na horní trojúhelníkovou
matici. Při převodu se používají ty úpravy, které nemění determinant, zejména
přičítání lineární kombinace ostatních řádků k danému řádku.
[
nahoru ]
![]() , sestavených
v m řádcích a n sloupcích:
, sestavených
v m řádcích a n sloupcích: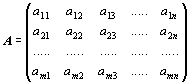 .
.![]() .
Prvky
.
Prvky ![]() pro
dané i tvoří i-tý řádek, prvky
pro
dané i tvoří i-tý řádek, prvky ![]() pro dané k tvoří k-tý sloupec. Řádky a sloupce se souhrnně
nazývají řady.
pro dané k tvoří k-tý sloupec. Řádky a sloupce se souhrnně
nazývají řady.![]() tvoří
hlavní diagonálu a nazývají se hlavní prvky, prvky
tvoří
hlavní diagonálu a nazývají se hlavní prvky, prvky ![]() tvoří
vedlejší diagonálu.
tvoří
vedlejší diagonálu.![]() ,
jestliže pod hlavní diagonálou jsou všechny prvky nulové, tzn.
,
jestliže pod hlavní diagonálou jsou všechny prvky nulové, tzn. ![]() .
.![]() ,
jestliže nad hlavní diagonálou jsou všechny prvky nulové, tzn.
,
jestliže nad hlavní diagonálou jsou všechny prvky nulové, tzn. ![]() .
.
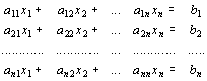
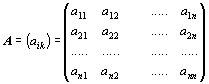 typu
typu  typu
typu 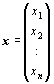 ,
resp.
,
resp. 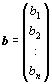 jako
vektor neznámých, resp. vektor pravých stran. Pak původní soustavu
můžeme zapsat v maticovém tvaru
jako
vektor neznámých, resp. vektor pravých stran. Pak původní soustavu
můžeme zapsat v maticovém tvaru