Exponenciální a logaritmická funkce, rovnice a nerovnice
Exponenciální funkce
Exponenciální funkcí
je každá funkce tvaru ![]() ,
kde
,
kde ![]() ,
, ![]() .
Číslo a je tzv. základ (jako u mocniny).
.
Číslo a je tzv. základ (jako u mocniny).
Poznámka:
Základní vlastnosti
exponenciální funkce: definována je pro všechna reálná čísla, je prostá, ryze
monotónní, pro ![]() rostoucí, pro
rostoucí, pro ![]() klesající, omezená pouze zdola (např. nulou), kladná, graf prochází body [0,
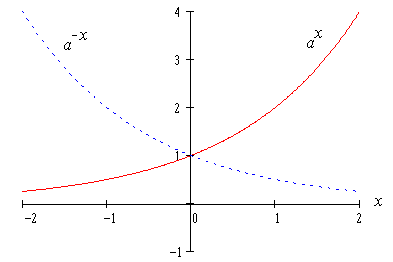
1] a [1, a]. Graf exponenciální funkce pro základ větší i menší než jedna
je na obrázku (
klesající, omezená pouze zdola (např. nulou), kladná, graf prochází body [0,
1] a [1, a]. Graf exponenciální funkce pro základ větší i menší než jedna
je na obrázku (![]() ):
Pro rychlou orientaci v různých problémech je bezpodmínečně nutné znát
jeho tvar zpaměti a umět si ho kdykoliv vybavit.
):
Pro rychlou orientaci v různých problémech je bezpodmínečně nutné znát
jeho tvar zpaměti a umět si ho kdykoliv vybavit.
Protože exponenciální
funkce ![]() vzniká
v podstatě z obecné mocninné funkce
vzniká
v podstatě z obecné mocninné funkce ![]() převedením proměnné ze základu do exponentu, platí pro ni obdobné věty jako
pro obecnou mocninu:
převedením proměnné ze základu do exponentu, platí pro ni obdobné věty jako
pro obecnou mocninu:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.

Logaritmická funkce
Logaritmickou funkcí
(logaritmem) při základu a nazýváme funkci inverzní k funkci
exponenciální (pro ![]() ,
,
![]() .).
.).
Matematický zápis: ![]() .
Slovně řečeno, “logaritmem čísla x při základu a je takové číslo
y, pro které platí, že x se rovná a na y”.
.
Slovně řečeno, “logaritmem čísla x při základu a je takové číslo
y, pro které platí, že x se rovná a na y”.
Poznámka:
Základní vlastnosti
logaritmické funkce: definována pouze pro kladná x, je prostá, pro ![]() rostoucí, pro
rostoucí, pro ![]() klesající, neomezená zdola ani shora, graf prochází body [1, 0], [a,
1]. Graf logaritmické funkce pro základ větší i menší než jedna je na obrázku
(
klesající, neomezená zdola ani shora, graf prochází body [1, 0], [a,
1]. Graf logaritmické funkce pro základ větší i menší než jedna je na obrázku
(![]() ). I jeho
tvar je nutné si dokonale zapamatovat.
). I jeho
tvar je nutné si dokonale zapamatovat.
Z definice logaritmické
funkce a vlastností exponenciální funkce se dají dokázat tyto, pro výpočty velmi
důležité věty, které platí pro každé ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() :
:
![]() ,
, ![]() ,
,
![]() ,
,
![]() nebo-li “logaritmus
součinu je roven součtu logaritmů”,
nebo-li “logaritmus
součinu je roven součtu logaritmů”,
![]() nebo-li “logaritmus
podílu je roven rozdílu logaritmů”, speciálně
nebo-li “logaritmus
podílu je roven rozdílu logaritmů”, speciálně ![]() ,
,
![]() nebo-li “logaritmus
k-té mocniny je roven k-násobku logaritmu”,
nebo-li “logaritmus
k-té mocniny je roven k-násobku logaritmu”,
![]() , což je vzorec
pro převod logaritmu na jiný základ, speciálně
, což je vzorec
pro převod logaritmu na jiný základ, speciálně ![]() .
.
Pozor!!! Obecně neplatí žádná obdobná věta o součinu, podílu nebo mocnině logaritmu, tzn. že “součin logaritmů není obecně roven logaritmu součinu”, “podíl logaritmů není obecně roven logaritmu podílu” a “mocnina logaritmu není obecně rovna logaritmu mocniny”. To je třeba si jasně uvědomit a odlišit tyto případy od platných vět uvedených výše!
Logaritmování a odlogaritmování výrazu
Logaritmovat (zlogaritmovat) výraz znamená vyjádřit jeho logaritmus pomocí logaritmů jednodušších výrazů, příp. proměnných. Používá se přitom zejména vět o logaritmu součinu, podílu a mocniny.
Příklad:
Logaritmujte při základu 10 výraz ![]() .
.
Řešení:
Aplikujeme operaci “log” na obě strany rovnice a upravíme podle uvedených vět:
![]() .
.
Odlogaritmovat výraz znamená vyjádřit výraz, jehož logaritmus je znám a je zapsán zpravidla pomocí logaritmů jednodušších výrazů, příp. proměnných. Používá se opět vět o logaritmu součinu, podílu a mocniny, tentokrát ale v obráceném směru.
Příklad:
Odlogaritmujte výraz ![]() .
.
Řešení: Můžeme použít dvě ekvivalentní metody:
Exponenciální rovnice
Exponenciální rovnicí nazýváme takovou rovnici, která obsahuje výraz s neznámou v exponentu kladného základu.
Obecná metoda řešení neexistuje, záleží na konkrétním tvaru, často je výhodný následující postup:
Příklad:
Řešte rovnici ![]() .
.
Řešení: Zlogaritmujeme obě strany přirozeným logaritmem (je možné
samozřejmě použít logaritmus o libovolném základu): ![]() .
Vzniklá rovnice je lineární a jejím řešením je
.
Vzniklá rovnice je lineární a jejím řešením je ![]() .
Vzniklý výraz již rozumně upravit nelze (!), maximálně jej můžeme převést na
tvar
.
Vzniklý výraz již rozumně upravit nelze (!), maximálně jej můžeme převést na
tvar ![]() , který
je ale pro číselný výpočet méně vhodný. Proveďme ještě zkoušku, i když jsme
použili pouze ekvivalentní úpravy a definičním oborem původních výrazů je R.
Procvičíme se tím v úpravě výrazu s logaritmy:
, který
je ale pro číselný výpočet méně vhodný. Proveďme ještě zkoušku, i když jsme
použili pouze ekvivalentní úpravy a definičním oborem původních výrazů je R.
Procvičíme se tím v úpravě výrazu s logaritmy: ![]()
![]() .
.
Logaritmická rovnice
Logaritmickou rovnicí nazýváme takovou rovnici, která obsahuje výraz s neznámou v argumentu logaritmické funkce.
Obecná metoda řešení neexistuje, záleží na konkrétním tvaru, často je výhodný následující postup:
Příklad:
Řešte v R rovnici: ![]() .
.
Řešení:
Pravou stranu upravíme: ![]() a odlogaritmujeme. Dostaneme lineární rovnici
a odlogaritmujeme. Dostaneme lineární rovnici ![]() ,
jejímž řešením je
,
jejímž řešením je ![]() .
Zkouška:
.
Zkouška: ![]() .
.
Exponenciální a logaritmické nerovnice
Exponenciální a logaritmické
nerovnice řešíme obdobně jako rovnice, tzn. převedeme na vhodný tvar a zbavíme
se exponenciální funkce, resp. logaritmu, zlogaritmováním, resp. odlogaritmováním.
Výslednou nerovnici řešíme vhodnou metodou. Při logaritmování, resp. odlogaritmování,
je ale nutné dávat pozor na znaménko nerovnosti, protože, jak už víme, exponenciála
a logaritmus jsou rostoucí pro ![]() a klesající pro
a klesající pro ![]() .
.
Proberme dva elementární příklady:
Příklad:
Řešte v R nerovnici ![]() .
.
Řešení:
Příklad:
Řešte v R nerovnici ![]() .
.
Řešení: