Dělení čísel na přirozená (značíme N), celá (Z), racionální (Q), iracionální (I), reálná (R) a komplexní (C) pokládáme za známé ze střední školy, stejně jako základní vlastnosti sčítání a násobení (komutativnost, asociativnost, distributivnost násobení vzhledem ke sčítání a pod.)

Zlomek je určitý druh zápisu podílu dvou čísel či výrazů: . Při provádění úprav výrazů se zlomky je nutné mít na paměti, že není definováno dělení nulou.

Rozšiřování zlomků: .

Krácení zlomků: .

Sčítání a odčítání zlomků: .

Násobení zlomků: .

Dělení zlomků: .

Složený zlomek: .

Odtud vidíme, že nejrychlejší převedení složeného zlomku na jednoduchý je vynásobení čitatele i jmenovatele složeného zlomku součinem jmenovatelů obou jednoduchých zlomků: .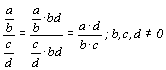

Absolutní hodnota reálného čísla a se značí a je definována takto: pro je , pro je . Platí (): ; ; ; ; .

Definici obecné mocniny reálného čísla s reálným exponentem je nutné “připravit” definicemi speciálnějších mocnin s přirozeným, celým a racionálním exponentem a definicí odmocniny. Je také nutné sledovat definiční obory jednotlivých operací, zejména to, zda je daná mocnina (odmocnina) definována i pro nulu, příp. záporný základ. Za každou definicí jsou uvedeny základní vlastnosti, které je bezpodmínečně nutné znát, protože na nich jsou založeny úpravy výrazů s mocninami a odmocninami.

Nechť , . Pak n-tou mocninou čísla a je číslo , kde v naznačeném součinu se a vyskytuje právě n-krát.

Nechť , . Je-li n = 0, pak pro definujeme . Je-li a , pak definujeme . Symbol je nyní definován pro každé a každé celé n.

Nechť , . Jestliže , pak n-tou odmocninou čísla a je takové kladné reálné číslo x, pro které platí . Toto číslo je právě jedno a značí se . Místo se píše . Pro se definuje . Jestliže a n liché, pak se definuje . Např. .

Pzn.: Pro n sudé platí tedy , nikoliv (obecně) , což platí pouze pro . Proto např. , nikoliv –2. V tom je nutné mít jasno. Např. exaktní řešení rovnice v R vypadá takto: .

Nechť je reálné číslo, r racionální číslo, které se dá (vždy) vyjádřit ve tvaru , kde p je celé a q přirozené číslo. Pak definujeme . Speciálně pro dostáváme , .

Nechť x je kladné reálné číslo, a libovolné reálné číslo. Pak existuje posloupnost racionálních čísel taková, že její limita je rovna a. Obecná mocnina se definuje jako limita posloupnosti , tj. limita posloupnosti mocnin s racionálním exponentem .

Polynomem (mnohočlenem) n-tého stupně proměnné x rozumíme (pro ) výraz .

Často je výhodný kratší zápis pomocí znaménka sumy:

Např. pro : .

Součinem dvou polynomů je polynom, který je součtem součinů všech členů prvního polynomu se všemi členy druhého polynomu: 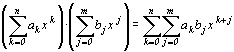. Speciálním případem je násobení polynomu reálným číslem k, tj. polynomem nultého stupně. Vznikne polynom, jehož koeficienty jsou rovny k-násobku původních hodnot.

Binomická věta je obecný vzorec pro libovolnou přirozenou mocninu dvojčlenu. Pro každé , platí: . Symboly jsou tzv. kombinační čísla. Např. .

Některé mnohočleny je možné vyjádřit jako součin mnohočlenů nižšího stupně. To má často velký význam, protože např. při úpravách zlomků tak můžeme získat možnost krácení. Obecný algoritmus na zjištění, zda je možné polynom rozložit na součin, neexistuje. Jedna možnost je určit tzv. kořeny polynomu a provést rozklad na součin kořenových činitelů (bude probráno později). Některé rozklady je potřeba znát zpaměti.

Např.: ; ; .

Pozor: v reálném oboru rozložit nelze!

Polynom stupně n lze dělit polynomem nižšího stupně m. Výsledkem může být opět nějaký polynom, pak se jedná o dělení beze zbytku, nebo součet polynomu a zlomku tvaru , kde je zbytek po dělení a je to polynom nižšího stupně než .

1. Dělenec i dělitel uspořádáme od nejvyšší mocniny x k nejnížší.
2. Vydělíme první člen dělence prvním členem dělitele; výsledkem je první člen podílu.
3. Vynásobíme tímto členem dělitele a výsledek odečteme od dělence; tím získáme nového dělence.
4. Opakujeme tento postup s novým dělencem tak dlouho, dokud není zbylý polynom nižšího stupně než dělitel. Tento zbylý polynom (pokud existuje) tvoří zbytek po dělení.

Př.: Proveďte naznačené dělení polynomů: .

---

---

---

(zbytek)

Výsledek lze interpretovat tak, že platí .

[ nahoru ]