Základy vektorové algebry

Úvod

Ze střední školy je znám pojem vektoru ve dvou základních významech: jednak tzv. geometrický vektor nebo-li orientovaná úsečka (úsečka s vyznačeným začátkem a koncem), jednak jako fyzikální veličina, která má určitý směr, orientaci a velikost. Oba významy mají společné znaky, mezi které patří zejména možnost sčítat (skládat) vektory a násobit je číslem, dále určovat velikost vektoru, úhel, který svírají dva vektory, rozkládat je na složky, určovat souřadnice atd.

Axiomatická definice vektoru abstrahuje od konkrétní představy a definuje vektor jako prvek vektorového (nebo také lineárního) prostoru:

Vektorový prostor

Vektorovým prostorem nad množinou reálných čísel (skalárů) R je neprázdná množina V, ve které jsou definovány dvě operace:

1. sčítání vektorů, které každé dvojici vektorů a, b z V přiřazuje vektor a + b
2. násobení vektoru skalárem, které každému skaláru k z R a vektoru a z V přiřazuje vektor ka.

Tyto operace musí splňovat následující podmínky:

1. a + b = b + a (komutativnost sčítání vektorů);
2. a + (b + c) = (a + b) + c (asociativnost sčítání vektorů);
3. existuje jediný vektor 0 takový, že 0 + a = a pro každé a z V (nulový vektor);
4. pro každý vektor a z V existuje jediný vektor -a takový, že a + (-a) = 0 (opačný vektor);
5. pro každé k, m z R a každý vektor a z Vplatí: k(ma) = (km)a (asociativnost násobení skalárem);
6. pro každé k, m z R a každý vektor a z Vplatí: (k + m)a = ka + ma (distributivní zákon);
7. pro každé k z R a každé a, b z Vplatí: k(a + b) = ka + kb (distributivní zákon);
8. pro každý vektor a z Vplatí: 1a = a (jednotkový prvek pro násobení skalárem).

Pozn.:

1. Uvedenou množinou skalárů může být také množina komplexních čísel C, obecně jakékoliv tzv. číselné těleso, což je jistá algebraická struktura, která je zobecněním pojmu množiny reálných čísel. Pro větší konkrétnost se bude dále hovořit o reálných číslech, ale pro většinu tvrzení není tento předpoklad nutný.
2. Nulový vektor se často značí obyčejnou nulou (skalární).

Př.: Typickým (a velmi důležitým) příkladem vektorového prostoru je n-násobný kartézský součin Rⁿ, tzn. množina všech uspořádaných n –tic reálných čísel, ve které jsou operace sčítání a násobení skalárem definovány takto:

(x₁, x₂, ..., x_n) + (y₁, y₂, ..., y_n) = (x₁ + y₁, x₂ + y₂, ..., x_n + y_n) ,

k (x₁, x₂, ..., x_n) = (kx₁, kx₂, ..., kx_n).

V semináři si dokážeme, že takto definované operace splňují výše uvedené podmínky.

Rozdíl vektorů

Na základě výše uvedené definice se dá dokázat, že ke každým dvěma vektorům a,b z V existuje právě jeden vektor x takový, že platí:

b + x = a.

Tento vektor se nazývá rozdílem vektorů a, b a značí se x = a – b. Platí: a – b = a + (-b). Odečíst vektor je tedy totéž co přičíst opačný vektor.

Lineární kombinace vektorů

Jestliže pro nějaký vektor x platí rovnost

x = k₁a₁ + k₂a₂ + … + k_na_n,

pak vektor x nazýváme lineární kombinací vektorů a₁, a₂, …, a_n s koeficienty k₁, k₂, …, k_n. Číslo n je lib. přirozené (a tedy konečné) číslo.

Lineární nezávislost množiny vektorů

Množina vektorů U daného vektorového prostoru se nazývá lineárně nezávislou, jestliže žádný její prvek x není lineární kombinací jiných prvků z U. V opačném případě je množina U lineárně závislá.

Báze vektorového prostoru

Bází vektorového prostoru nazýváme takovou jeho podmnožinu B, pro kterou platí:

1. B je lineárně nezávislá množina;
2. každý vektor x z V lze vyjádřit jako lineární kombinaci vektorů z B.

Počet prvků báze B daného vektorového prostoru V nezávisí na konkrétní volbě báze a nazývá se dimenzí vektorového prostoru. Značí se obvykle dim(V).

Pzn.

1. Dimenze může být konečná,tzn. rovna nějakému přirozenému číslu n, nebo nekonečná.
2. Místo pojmu “počet prvků” je přesnější pojem “kardinální číslo”, který je obecnější a lze jej použít právě na případ nekonečných množin. Pro konečné množiny jsou oba pojmy totožné.
3. Je-li báze B prostoru V tvořena n vektory b₁, b₂, …, b_n, pak vektor x = k₁b₁ + k₂b₂ + … + k_nb_n , kde n-tice čísel k₁, k₂, …, k_n je určena jednoznačně. Libovolný vektorový prostor V dimenze n je tedy možno vzájemně jednoznačně zobrazit na množinu všech uspořádaných n-tic reálných čísel Rⁿ. Mluvíme pak o souřadnicích vektoru x v bázi B. Volba báze znamená vlastně volbu souřadného systému. Odtud také plyne nepřesná formulace, že “vektor je n-tice čísel”.

Př. V prostoru R³ jsou bází např. množiny vektorů B₁ = {(1, 0, 0), (0, 1, 0), (0, 0, 1)}, B₂ = {(12, 0, 0), (0, -4.2, 0), (0, 0, 8.4)}, B₃ = {(1, 1, 0), (0, 1, -1), (1, 1, 1)} apod.

Norma (velikost, délka, modul) vektoru

Normou vektoru rozumíme reálnou funkci na vektorovém prostoru V, platí-li pro libovolné dva vektory x, y z V a lib. skalár k:

1. (pozitivnost)
2. (trojúhelníková nerovnost)
3. (homogenita)
4. 

Pzn.

1. Často se norma značí dvěma svislými čarami, čímž se odliší od označení absolutní hodnoty reálného, příp. komplexního čísla, ale z  kontextu je vždy zřejmé, o co jde, proto se přikláním k jednoduššímu zápisu.
2. Norma indukuje tzv. metriku, tj reálnou funkci d(x,y) vektorů x, y z V takto: d(x,y) =

Př. Typickým příkladem normy je tzv. Euklidovská norma, definovaná v Rⁿ jako odmocnina ze součtu druhých mocnin souřadnic vektoru, která je v případě geometrických vektorů totožná s jejich délkou:

.

Skalární (vnitřní) součin vektorů

Skalárním součinem nazveme funkci, která dvojici vektorů x, y z V přiřazuje skalár, označený tak, že pro každé x, y, z z V a každý skalár k platí:

1. (aditivnost)
2. (homogenita)
3. (symetrie, komutativnost)
4. pro (pozitivní definitnost).

Jednoduchým důsledkem uvedených axiomů je dále:

5. 
6. 
7. .

Pzn.

1. Tato definice platí přesně pouze pro vektorový prostor nad tělesem reálných čísel, pro případ komplexních čísel by v relacích ad3) a ad6) byly malé změny.
2. Dá se dokázat, že reálná funkce

Př. Typickým příkladem vektorového prostoru se skalárním součinem je opět 2 nebo 3-dimenzionální prostor geometrických, příp. fyzikálních vektorů, ve kterém je skalární součin vektorů a, b definován jako jako součin velikostí (norem) těchto vektorů a kosinu úhlu, který svírají: . Odtud se přejímá pro libovolné vektorové prostory pojem kolmosti vektorů: dva nenulové vektory x, y z V jsou na sebe kolmé právě tehdy, jestliže jejich skalární součin je roven nule.

Ortogonální a ortonormální báze

Ortogonální bází vektorového prostoru V, vybaveného skalárním součinem, označujeme takovou bázi, jejíž vektory jsou navzájem kolmé, tzn. jejich skalární součin je nulový. Mají-li navíc všechny vektory báze jednotkovou velikost (nebo-li jsou normovány k 1), mluvíme o ortonormální bázi.

Konkrétněji: je-li B = { b₁, b₂, …, b_n} ortonormální bází, pak platí pro skalární součin lib. dvou jejích prvků b_i, b_j vztah: , kde symbol na pravé straně, tzv. Kroneckerovo delta, je roven 1 pro i = j, jinak je roven 0.

Př. Z výše uvedených bází prostoru R³ je B₁ ortonormální, B₂ (pouze) ortogonální a B₃ obecná.

Skalární součin v ortonormální bázi

Nechť je dán vektorový prostor V se skalárním součinem a jeho ortonormální báze B = {b₁, b₂, …, b_n} (pro jednoduchost uvažujme konečněrozměrný prostor). Libovolné vektory x, y z V lze, jak již víme, psát jednoznačně ve tvaru x = k₁b₁ + k₂b₂ + … + k_nb_n, y = m₁b₁ + m₂b₂ + … + m_nb_n. Skalární součin těchto vektorů lze při využití jeho aditivnosti a homogenity lehce vyjádřit ve tvaru

,

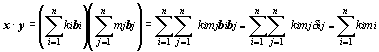což je známý tvar výpočtu skalárního součinu jako součtu součinů odpovídajících si souřadnic.

Průmět a projekce vektoru

Průmětem vektoru a do vektoru b rozumíme vektor , kde je jednotkový vektor ve směru vektoru b. Číslo nazýváme projekcí vektoru a do vektoru b.

Pzn.

1. V případě geometrických nebo fyzikálních vektorů v 2 a 3-dimenzionálním prostoru se dá projekce vektoru a do vektoru b vyjádřit ve tvaru , kde g je úhel mezi vektory a, b, ze kterého je zřejmý původ zavedené terminologie.
2. Za pozornost dále stojí, že souřadnice vektoru v libovolné ortonormální bázi je totožná s projekcí tohoto vektoru do příslušného bázového vektoru.

Vektorový součin

Vektorovým součinem vektorů a, b z 3-dimenzionálního vektorového prostoru V rozumíme vektor, který je pravotočivě kolmý k vektorům a, b a jehož velikost je rovna, kde g je úhel mezi vektory a, b.

Pzn.

1. Vektorový součin se značí, jak už bylo ukázáno, křížkem , na rozdíl od skalárního součinu, který se značí tečkou. Není tedy možno tyto symboly zaměňovat, jak to je možné u obyčejného součinu dvou skalárů.
2. Vektorový součin je definován pouze v třírozměrném prostoru, protože při menší dimenzi by neexistoval žádný vektor, vyhovující definici, a při větší naopak více než jeden, definice by nebyla jednoznačná. Jedná se tedy o daleko méně obecný pojem, než je např. skalární součin.
3. Pravotočivě kolmý znamená, že směr výsledného vektoru je dán pravidlem pravé ruky: položíme pravou ruku malíčkovou hranou na rovinu vektorů a, b tak, že prsty vymezují ostrý úhel od vektoru a k vektoru b, pak vztyčený palec pravé ruky ukazuje směr vektorového součinu vektorů a, b.
4. Vektorový součin je podobně jako skalární součin aditivní a homogenní, avšak není komutativní, nýbrž tzv. antikomutativní,tzn. při změně pořadí činitelů se změní jeho znaménko (orientace se změní na opačnou).
5. V ortonormální bázi se pro souřadnice vektorového součinu dá odvodit:

.

6. Geometrický význam vektorového součinu je ten, že jeho velikost je rovna obsahu rovnoběžníku určeného vektory a, b.

[ nahoru ]