1.2.1 Exponenciální funkce 
Definice
Exponenciální funkcí (zkráceně exponenciálou)
je každá funkce tvaru 
, kde 
, 
, 
. Číslo a
je tzv. základ, 
exponent.
Poznámka
a)
Jedná se vlastně o obecnou mocninu 
s přehozeným
významem veličin a 
. U obecné mocniny
je proměnnou základ a parametrem exponent, u exponenciální funkce je pevným
parametrem základ a exponent proměnnou.
b)
Základ 
vylučujeme z toho
důvodu, že funkce 
je funkce konstantní
a má některé vlastnosti dosti odlišné od vlastností ostatních exponenciálních
funkcí, nikoliv proto, že by tento výraz nebyl dobře definován.
c)
Zvláštní význam má exponenciální funkce, jejíž základ je tzv. Eulerovo
číslo nebo-li přirozený základ 
(iracionální číslo).
Kromě zápisu 
se pro ni často
používá zápis 
, zvláště tehdy,
má-li exponent složitější strukturu.
Graf exponenciální funkce.
Graf exponenciální funkce pro základ větší
i menší než jedna je na obrázku ( 
): Pro rychlou
orientaci v různých problémech je bezpodmínečně
nutné znát jeho tvar zpaměti a umět si ho kdykoliv vybavit.
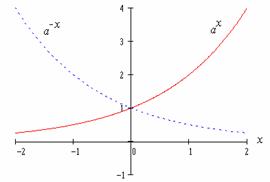
Základní vlastnosti exponenciální funkce.
Věta
Exponenciální funkce je definována pro všechna reálná čísla, je prostá, ryze
monotónní, pro 
rostoucí, pro
klesající, omezená
pouze zdola (např. nulou), kladná, graf prochází body
[0, 1] a [1, a].
Důležité vzorce.
Věta
Pro každé 
, 
platí:
,
, 
, 
, 
, 
.