6.7.3 Délka parametricky zadané křivky

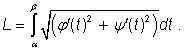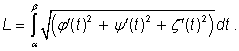Zadání

Určete délku  L  křivky zadané v rovině parametrickými rovnicemi  a , kde parametr  a vektorová funkce je prostá na [1].

Řešení

Postup řešení je obdobný tomu, který jsme nastíněn v kapitole věnované výpočtu délky grafu funkce. Interval    nejdříve rozdělíme dostatečně jemným dělením    a na každém z dělicích intervalů    považujeme křivku s přibližnou platností za úsečku s koncovými body    a  .  I nyní počítáme v prvním přiblížení délku oblouku  L  jako součet délek těchto elementárních úseček  ,  kde    a  .   Platí tedy [2]

,

kde   .  Protože    a    jsou obecně různá, nezískali jsme v tomto případě „čistou“ Riemannovu integrální sumu. Přesto je však možno ukázat, že platí (viz např. učebnice Havlíčkova [2])

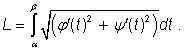
Poznámka

Obdobný vzorec lze odvodit i pro křivku zadanou parametrickými rovnicemi v prostoru ,  a  :


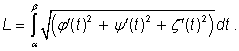
[1] Křivka tedy v žádném bodě neprotíná sama sebe, nanejvýš může mít stejný počáteční a koncový bod.

[2] V úpravách využíváme Lagrangeovu větu o přírůstku:   a  .  Všimněte si, že body v nichž počítáme derivace jsou pro  j  a  y  různé.