3. Protokol o měření

3.1 Struktura protokolu o měření

Z každého uskutečněného měření je nutné vypracovat protokol. Tento protokol má dvě základní funkce. Jednak informuje o průběhu a hlavních výsledcích měření, jednak je dokladem o tom, kým a kdy bylo měření provedeno.

Správně vypracovaný protokol by měl obsahovat následující údaje:

  1. jméno autora a spolupracovníka;
  2. datum měření;
  3. úkol měření;
  4. stručnou teorii měřící metody;
  5. postup měření;
  6. naměřené hodnoty;
  7. vypočtené hodnoty;
  8. určení přesnosti měření;
  9. závěr.

Ve zbývajících kapitolách rozebereme několik problémů, které se při vypracování protokolu o měření nejčastěji objevují.

3.2 Zápis výpočtů do protokolu o měření

U většiny měřících úloh je třeba z daných, zpravidla přímo naměřených hodnot, vypočítat hodnoty jiných veličin, které nás zajímají. Do protokolu o měření zapisujeme výpočet tak, že nejprve uvedeme obecný výpočetní vztah (vzorec s proměnnými), pak vzorec s dosazenými hodnotami za jednotlivé proměnné a nakonec vypočtenou hodnotu, vhodně zaokrouhlenou.

Příklad.

Výpočet obrazové ohniskové vzdálenosti  pomocí předmětové vzdálenosti  a obrazové vzdálenosti :

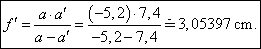
Z výpočtu zapsaného podle uvedených pravidel lze vyčíst všechny potřebné údaje, tzn. použitý výpočetní vztah, hodnoty dosazených veličin a vypočtenou hodnotu. Při kontrole je tudíž možné celý výpočet zopakovat. Pokud k tomu není konkrétní důvod, neuvádějí se žádné mezivýsledky. Ve výsledku se ponechává dostatečný počet platných cifer, který se zmenší teprve po stanovení nejistoty měření (viz dále).

Pokud se podle stejného vzorce počítá větší počet hodnot (organizovaných zpravidla v tabulce), provede se výše uvedeným způsobem pouze výpočet první hodnoty, který slouží také jako příklad výpočtu ostatních hodnot.

3.3  Určení přesnosti měření

Určení přesnosti měření výpočtem nejistoty naměřených hodnot se obyčejně považuje za zbytečnou a otravnou činnost. Rád bych Vás přesvědčil, že tomu tak není.

Není asi sporu o tom, že žádné měřící zařízení neměří absolutně přesně (alespoň měříme-li spojité, tj. nediskrétní veličiny). Dejme tomu, že pomocí nějakého zařízení naměříme hodnotu určité veličiny 5 jednotek. Pokud nevíme, jak přesné je měřící zařízení, nevíme o skutečné hodnotě dané veličiny absolutně nic. Může to být 5,1 nebo 3,68, ale třeba i 100. Teprve máme-li alespoň hrubou představu o přesnosti měření, např. víme-li, že u běžných laboratorních měření je velikost chyby měření zpravidla menší než pět procent naměřené hodnoty, může nám být naměřená hodnota 5 užitečná, neboť víme, že skutečná hodnota by se od naměřené neměla lišit o více než 0,25 jednotky.

V tomto kurzu nám ovšem tak hrubý odhad přesnosti měření stačit nebude. U většiny úloh je třeba tzv. nejistotu výsledné veličiny přesně vypočítat. K tomu existuje poměrně rozsáhlá teorie, kterou v případě zájmu naleznete v doporučené literatuře. My se omezíme pouze na jednoduchý výklad.

3.3.1 Chyba měření

Chybou měření veličiny  rozumíme hodnotu

, (1)

kde  je naměřená hodnota veličiny  a  je skutečná hodnota veličiny .

Poznamenejme, že skutečnou hodnotu  většinou neznáme, ale zde i dále stačí předpokládat, že existuje. Někdy lze za skutečnou hodnotu pro určité měření považovat hodnotu, naměřenou několikanásobně přesnější metodou.

Chyby měření dělíme do tří kategorií. Chyby hrubé jsou zapříčiněny nepozorností obsluhy nebo poruchou přístroje a projeví se zpravidla vysoce nepravděpodobnou hodnotou naměřené veličiny, která se výrazně liší od jiných naměřených hodnot nebo od hodnoty očekávané na základě zkušenosti. Naměřené hodnoty zatížené hrubou chybou z měření vyškrtáváme. Hrubé chyby v dalším textu již neuvažujeme.

Chyby systematické (značka ) mají stále stejnou hodnotu. To znamená, že při opakovaných měřeních téže veličiny za stejných podmínek se naměřená hodnota nemění a je o pevnou hodnotu odlišná od přesné hodnoty.

Příklad.

Špatně nakalibrovaný digitální voltmetr může místo správné hodnoty 6 V trvale ukazovat hodnotu třeba 6,18 V, tzn. systematická chyba je zde V.

Chyby náhodné (značka ) nelze z měření zcela vyloučit, jejich hodnota kolísá případ od případu podle určitého zákona rozdělení (např. Gaussova zákona).

Výsledná chyba provedeného měření je dána součtem systematické a náhodné chyby:

. (2)

Chyba  se označuje přesněji jako absolutní a má rozměr měřené veličiny, oproti tzv. relativní chybě , která je bezrozměrná a je definována vztahem

, (3)

tedy jako poměr příslušné absolutní chyby měření  a velikosti skutečné hodnoty . Relativní chyba se udává obvykle v procentech.

3.3.2 Maximální možná chyba přístroje

Jak už bylo řečeno, nemůžeme většinou zjistit přímo chybu měření, protože neznáme skutečnou hodnotu měřené veličiny. Můžeme se ale pokusit velikost chyby odhadnout, na což existuje rozsáhlá teorie. Pro naše účely se omezíme pouze na jeden speciální druh odhadu chyby měření.

U většiny přístrojů udává výrobce tzv. maximální možnou chybu přístroje. Pokud je přístroj v pořádku, lze říci, že skutečná hodnota se od naměřené nemůže lišit o hodnotu větší než je tato maximální chyba. Skutečná chyba konkrétního přístroje při určitém měření může být menší nebo rovna maximální možné chybě a svou povahou může patřit do kategorie systematických chyb (častější případ, způsobený např. nepřesnou kalibrací) nebo i nahodilých chyb (méně často).

V případě, že údaj o maximální chybě není k dispozici, lze u přístrojů se stupnicí použít tzv. půldílkové pravidlo:

Maximální možná chyba je zhruba dána hodnotou poloviny nejmenšího dílku stupnice.

 

Příklad.

Např. při měření vzdálenosti dvou rysek milimetrovým měřítkem můžeme volit maximální možnou chybu rovnu polovině milimetru, při měření krejčovským metrem půl centimetru.

Obecně lze říci, že stanovení maximální možné chyby daného měření vyžaduje také určitou zkušenost a fyzikální cit.

Příklad.

Hledáme-li např. obrazovou vzdálenost posouváním stínítka do polohy, kdy se obraz jeví maximálně ostře, nemusí být maximální možná chyba dána půldílkovým pravidlem. Může se stát, že obraz je viditelný stejně ostře v určitém rozmezí poloh. Pak je správnější vzít jako maximální možnou chybu měření vzájemnou vzdálenost obou krajních poloh, ve kterých se obraz ještě jeví ostře.

3.3.3 Nejistota měření

Chyba měření teoreticky umožňuje kvantitativní porovnání přesnosti různých výsledků měření, ale pouze tehdy, známe-li správnou hodnotu . Protože, jak bylo řečeno výše, tomu tak většinou není, je nutné umět odhadnout maximální možnou velikost absolutní chyby. Nově byl zaveden pojem nejistoty měření.

Nejistotou měření veličiny  rozumíme parametr , přidružený k výsledku měření, který charakterizuje rozptyl hodnot, které lze důvodně přisoudit měřené veličině.

Zpravidla se jedná o pološířku intervalu , ve kterém se skutečná hodnota  vyskytuje s určitou pravděpodobností (např. 68% u tzv. standardních nejistot za předpokladu normálního rozdělení náhodných chyb). Střed intervalu  představuje nejlepší odhad skutečné hodnoty  a je buď roven naměřené hodnotě nebo aritmetickému průměru z více naměřených hodnot (v případě výskytu náhodných chyb).

3.3.4 Standardní nejistota měření typu A

U tohoto typu nejistot vycházíme ze statistického zpracování série opakovaných měření téže veličiny, zatížených náhodnou chybou. Provedeme-li celkem  nezávislých měření, obdržíme  obecně různých hodnot . Výsledná naměřená hodnota (nejlepší odhad skutečné hodnoty) je dána aritmetickým průměrem

. (3)

Standardní nejistota měření (za předpokladu dostatečně velkého ) se vypočte podle vzorce

. (4)

Jedná se vlastně o tzv. směrodatnou odchylku aritmetického průměru naměřených hodnot.

3.3.5 Standardní nejistota měření typu B

Jedná se o určení nejistoty měření jinak než statistickou analýzou série měření. Nejčastěji jde o stanovení nejistoty měření zatíženého systematickými (ale i náhodnými) chybami z jednoho nebo více zdrojů nejistoty.

Jestliže se na výsledné hodnotě měření veličiny  podílí  zdrojů nejistoty se známými standardními nejistotami ,  , pak nejistota této veličiny je dána vztahem

, (5)

kde  jsou součinitele (koeficienty) citlivosti jednotlivých zdrojů nejistoty.

My budeme v tomto praktiku používat vztah (5) zejména pro výpočet nejistoty veličiny nepřímo měřené, tzn. veličiny vypočítávané z jiných naměřených veličin.

Nechť nepřímo měřená veličina  je funkcí  hodnot přímo měřených nebo jinak stanovených veličin , . Jako naměřenou hodnotu (nejlepší odhad skutečné hodnoty) veličiny  vezmeme hodnotu funkce  v naměřených hodnotách  veličin :

. (6)

K určení nejistoty veličiny  použijeme vztah (5), kde součinitelé citlivosti  jsou nyní totožní s parciálními derivacemi :

. (7)

Všechny derivace vyhodnocujeme v bodě odpovídajícím naměřeným hodnotám  veličin .

Příklad.

Veličina  byla naměřena s výsledkem  jednotek a s nejistotou  jednotek, veličina  má naměřenou hodnotu  jednotek s nejistotou  jednotek. Nepřímo měřená veličina  má v odpovídajících jednotkách hodnotu

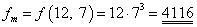
a nejistota měření je

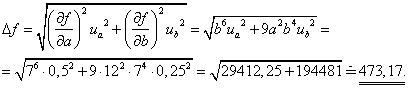
Získaný výsledek správně zapíšeme ve tvaru  nebo  příslušných jednotek (viz následující kapitolu). Zkuste uvážit, která veličina z dvojice ,  přispívá k celkové nejistotě veličiny  větším dílem.

3.3.6 Kombinovaná a rozšířená nejistota měření

V praxi je často nutné podchytit v nejistotě měření oba výše uvedené typy nejistot. To nastává např. u měření, zatíženého jak náhodnou chybou (projevující se fluktuacemi naměřených hodnot), tak i systematickou chybou měřidla (jejíž maximální možnou velikost nalezneme obvykle v návodu k použití měřidla nebo použijeme výše uvedené půldílkové pravidlo).

Jestliže nejistota typu A má hodnotu  a nejistota typu B hodnotu , pak výsledná, tzv. kombinovaná nejistota veličiny  je dána vzorcem

. (8)

Výše uvedené standardní nejistoty definují (za předpokladu normálního rozdělení chyb) pološířku intervalu, ve kterém se skutečná hodnota nachází s pravděpodobností přibližně 68%. Pro dosažení vyššího pokrytí je nutné tento interval rozšířit, tzn. vynásobit standardní nejistotu  koeficientem rozšíření  větším než jedna. Tím dostaneme tzv. rozšířenou nejistotu :

. (9)

Za předpokladu normálního rozdělení chyb obdržíme pro  zhruba 95%-ní rozšíření a pro  téměř 100%-ní (přesněji 99,7%-ní) rozšíření. Tento poslední případ budeme v našem praktiku používat přednostně.

Příklad.

Z 10 opakovaných měření doby kyvu kyvadla byla vypočtena metodou A výsledná hodnota 6,4526 s se standardní nejistotou 0,0218 s. Výrobce udává maximální možnou chybu údaje stopek 0,01 s. Hledejme trojnásobně rozšířenou kombinovanou nejistotu měření.

Údaj 0,01 s lze ztotožnit s trojnásobně rozšířenou nejistotou typu B, proto standardní nejistota daná zřejmě systematickou chybou stopek je . Protože standardní nejistota dalšího zdroje chyb (zřejmě lidského faktoru) je , dostáváme podle vzorců (8) a (9) pro výslednou, trojnásobně rozšířenou kombinovanou nejistotu výsledku hodnotu

.

Naměřenou hodnotu doby kyvu  kyvadla správně napíšeme (viz další podkapitolu) ve tvaru  s. Slovně lze výsledek formulovat tak, že skutečná hodnota doby kyvu kyvadla se prakticky musí nacházet v nalezeném intervalu. Pokud tomu tak není, došlo k hrubé chybě nebo jsme přehlédli další podstatný zdroj nejistoty měření.

3.3.7 Zápis naměřené veličiny včetně nejistoty

Naměřené veličiny včetně nejistoty zapisujeme ve tvaru

 (10)

kde  je hodnota přímo nebo nepřímo naměřená a  je nejistota měření zadaného typu (v tomto praktiku většinou trojnásobně rozšířená nejistota typu B).

Vzniká otázka, kolik platných míst v zápise (10) uvádět. Je zřejmé, že počet platných míst výsledku by měl korespondovat s přesností měření, tzn. velikostí nejistoty měření. Víme-li například, že nejistota měření určité délky je jeden milimetr, nemá cenu uvádět naměřenou délku na tisíciny milimetru.

Platí jednoduché pravidlo:

Nejistotu měření  zaokrouhlujeme nahoru na jedno, maximálně dvě platná místa a naměřenou hodnotu  zaokrouhlujeme tak, aby její nejnižší zapsaný řád odpovídal nejnižšímu zapsanému řádu nejistoty měření.


Příklad.

Správně zapsané jsou tyto naměřené hodnoty:

, , , .

Chybně zapsané jsou následující naměřené hodnoty:

, , .

3.4 Závěr protokolu o měření

Závěr je nejdůležitější částí protokolu o měření. Uvědomte si, že většina čtenářů Vašeho protokolu bude číst zejména jeho závěr. Závěr by měl být přehledný a měl by obsahovat: